Wybory
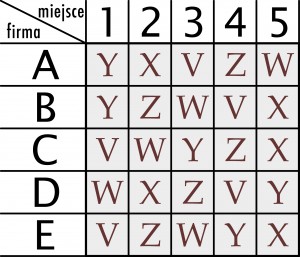
Do fotela prezydenckiego kandydowało pięć osób – V, W, X, Y, Z. Stawka była bardzo wyrównana. Pięć firm (A, B, C, D, E) przeprowadziło sondaże tuż przed wyborami, a ich wyniki różniły się. W tabeli przedstawiono kolejność kandydatów w poszczególnych sondażach, zgodną z liczbami głosów oddanych na każdego.
Po wyborach okazało się, że żadna z tych kolejności nie była zgodna z wynikiem wyborów, ale każda pozycja została trafiona w co najmniej jednym sondażu (trafieniem jest wskazanie właściwego kandydata na właściwym miejscu). Ponadto cztery sondaże zawierały tyle samo trafień, a jeden o jedno trafienie mniej.
Jakie były wyniki wyborów, czyli którzy kandydaci znaleźli się na kolejnych miejscach?

Komentarze
Wyszło mi: VXWZY
To będzie vxwzy, ale przegrzałem zwoje (niewiele dziś trzeba).
vwxzy
Szwagier chciał pomóc i przypomniał mi ten wpis
http://penszko.blog.polityka.pl/2016/02/23/para-komplementarna/
Jednakowoż poradziłem sobie bez tego.
W czasie meczu było dużo czasu na myślenie.
VXWZY
Znalezione w głowie: VXWZY
1. V
2. X
3. W
4. Z
5. Y
Pozdrawiam, Ola
Kolejność VXWZY.
Drogą eliminacji: z 5! = 120 możliwości odrzucamy te, które nie pasują (np. te z X, Z na pierwszym miejscu, itd), a także oczywiście 5 podanych, i zostaje tylko 10, z których jedna spełnia ostatni warunek: cztery sondaże przepowiadają po dwie pozycje, jeden jedną.
W pamięci znalazłem VXWZY, a rozumowałem następująco:
maksymalna liczba trafień to 11 (YZWVX). Stąd cztery sondaże mają po 2 trafienia i jeden jedno. Zakładając X na pozycji 5 i biorąc po kolei wszystkie 3 możliwości na poz. 4 widać, że nie ma prawidłowego rozwiązania. Zatem X jest na poz. 2. Z poz. 1 Y i W nie dają rozwiązania. Dalej już z górki 🙂
Komputer potwierdził, że jedynym rozwiązaniem jest: VXWZY.
Zadanie jest dość proste, nawet jeśli chce się je robić ręcznie. W najgorszym wypadku do sprawdzenia mamy 5! = 120 możliwości, z których na pierwszy rzut oka większość odpada.
„każda pozycja została trafiona w co najmniej jednym sondażu” => było w sumie co najmniej 5 trafień.
„cztery sondaże zawierały tyle samo trafień, a jeden o jedno trafienie mniej” => suma trafień wyraża się liczbą 5k + 4, czyli (uwzględniając poprzednie spostrzeżenie) suma trafień wynosi co najmniej 9.
Na pierwszych 4 miejscach każdy kandydat występuje co najwyżej 2 razy, na 5 miejscu 3 razy => łączna suma trafień nie przekracza 4*2+3 = 11 => suma trafień to dokładnie 9.
Teraz robimy tak:
1. Zakładamy, że na 5 miejscu nie została trafiony kandydat X (występujący 3 razy). Czyli na piątym miejscu mamy kandydata, który występuje raz. To oznacza, że na każdym miejscu od 1 do 4 musiał znaleźć się kandydat występujący na tym miejscu w dokładnie dwóch sondażach. To dość szybko ręcznie prowadzi do rozwiązania VXWZY.
2. Jeśli na 5 miejscu znajduje się kandydat X, to na miejscach od 1 do 4 dla dwóch miejsc musi być kandydat występujący w dwóch sondażach oraz dla dwóch pozostałych kandydat występujący w jednym sondażu. Tego przypadku już nie analizowałem ręcznie, ale podejrzewam, że dość szybko udałoby się wyeliminować wszystkie możliwości, nie uzyskując rozwiązania w tym przypadku.
Kolejność była następująca VXWZY
B jedno trafienie, pozostałe po dwa. Gdyby każda firma trafiła tyle samo razy to rozwiązaniem jest: XVWZY.
Jedyny możliwy wynik wyborów: VXWZY
Brute force z excelem (120 kombinacji):
V X W Z Y
+ ławo można wyeliminować kilka(-dziesiąt) kombinacji
Pozdrawiam
Ciekawa jest eliminacja wg liczby trafien.
Jesli cztery sondaze zawieraly tyle samo trafien a jeden o jedno mniej to mozna na wstepie wyeliminowac z 5go miejsca wartosc X (3 trafienia) i wiemy ze 5te miejsce mialo 1 trafienie (Y lub W). Z tego wynika ze miejsca 1-4 maja 2 trafienia (o 1 wiecej) czyli 1 pozycja to V lub Y, 2 pozycja to X lub Z, 3cia to W (jedyne rozwiazanie), czwarta to Z lub V, no a piata juz znamy.