Bycze rekuto
Rekuto gościło w Łamiblogu przed niespełna miesiącem. Przypomnę na czym polega.
Diagram należy podzielić wzdłuż linii przerywanych na prostokąty – w każdym powinna się znaleźć jedna liczba równa połowie jego obwodu, czyli sumie długości dwóch sąsiednich boków (jednostką długości jest bok kratki).
Przykład:
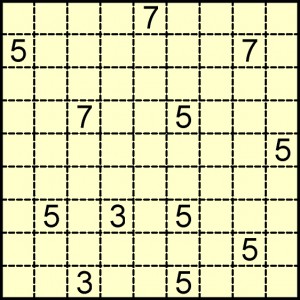
Powracam do tej łamigłówki ze względu na ciekawe zadanie, które otrzymałem od Michała S. – jest nim poniższe rekuto, które… nie ma rozwiązania.
Rozwiązując łatwo się przekonać, że w diagramie tkwi byk, ale chodzi o coś innego: Michał napisał, że nierozwiązywalność tego zadania widoczna jest „na pierwszy rzut oka”. Ja bym napisał nieco inaczej: proszę podać dowód nierozwiązywalności, oczywiście nie zabierając się w ogóle za rozwiązywanie.
I dodatkowe zadanie: proszę zmienić tylko jedną liczbę (nie zmieniając jej miejsca) tak, aby rekuto miało rozwiązanie.


Komentarze
Jeśli suma jest nieparzysta, to jeden z boków musi być liczbą parzystą, drugi nieparzystą. A to daje parzyste pole prostokąta. W zadaniu wszystkie liczby są nieparzyste, więc suma składowych prostokątów musiałaby być również parzysta, jednak długość boku całego kwadratu jest równa 9.
Póki co nie proponuję poprawki 🙂
Wszystkie liczby są nieparzyste i >1. Jeśli przedstawimy taką liczbę nieparzystą jako sumę dwóch liczb naturalnych, to jedna będzie parzysta, a druga nieparzysta, nie ma innej możliwości. Pole będzie więc takiego prostokąta liczbą parzystą. Suma pól też, a tu jest 9×9, czyli 81.
Nieparzystość każdej sumy rodzi parzystość iloczynów, których sumy nie da się wpasować w nieparzystość uniwersum.
środkową piątkę w 6. kolumnie trzeba zamienić na 6
Diagram składa się z 81 kratek (9×9), zatem w dowolnym jego podziale na prostokąty musi pojawić się przynajmniej jeden prostokąt o nieparzystym polu, taki prostokąt ma oba boki długości nieparzystej co oznacza, że połowa obwodu tego prostokąta jest parzysta, a to niemożliwe bo w diagramie nie ma liczb parzystych.
Z powyższego wynika od razu wskazówka do drugiego zadania. Nowa liczba musi być parzysta, a prostokąt zawierający tę liczbę musi mieć oba boki nieparzyste.
Pole powierzchni całego diagramu wynosi 81 kratek.
Pole powierzchni prostokąta o sumie długości i szerokości równej 7 wynosi:
1×6=6 ,2×5=10 albo 3×4=12
Pole prostokąta dla 5 wynosi:
1×4 albo 2×3=6
Pole prostokąta dla 3 wynosi
1×2=2
Suma liczb parzystych nie da 81
Trzeba 3 z ostatniego rzędu zamienić na 4.
Dowodu nierozwiązywalności nie umiem podać, ani wskazać bez rozwiązywania, co nie pasuje. Inna sprawa rozwiązać i zmienić na koniec jedną liczbę, to było bardzo proste:
http://pokazywarka.pl/399hn2/
Każda liczba w diagramie to prostokąt o określonych długościach boków:
„3” to prostokąt 2×1
„5” to prostokąt 4×1 lub 3×2
„7” to prostokąt 6×1, 5×2 lub 4×3
Ponieważ pole kwadratu stanowiącego diagram, który należy wypełnić 12 prostokątami wynosi 81, to podanymi prostokątami nie można go wypełnić. Uzasadnienie tego faktu jest proste. Maksymalna suma pół prostokątów wynosi 82 i nie można jej zmniejszyć o 1 a tylko o 2 kwadraciki. Gdy jeden z prostokątów „5” będzie miał wymiary 4×1 (a nie 3×2) to wówczas wystarczy powiększyć jeden z prostokątów „3” o 1. Jeżeli powiększymy prostokąt „3” z trzeciego wiersza od dołu wówczas rekuto ma jedno rozwiązanie. Gdy powiększymy „3” z najniższego wiersza to rekuto ma 4 rozwiązania.
Rozwiązanie
http://pokazywarka.pl/p9bgya/
Pole prostokąta o połówce obwodu będącym liczbą nieparzystą jest liczbą parzystą. W diagramie są rozmieszczone tylko liczby nieparzyste, zaś jego pole jest liczbą nieparzystą, więc nie da się go wysumować z pól prostokątów o podanych wymiarach.
Zamienić można w trzecim wierszu od dołu prawą 5 na 6; albo 3 w dolnym wierszu na 4 (i wtedy rozwiązania są dwa!), lub drugą 3 na 4. Są jakieś inne? 🙂
Nieparzystą sumę długości boków można uzyskać tylko wtedy, gdy długość jednego boku prostokąta będzie liczbą parzystą, a druga nieparzystą. Pola takich prostokątów są liczbami parzystymi. Suma zaś liczb parzystych jest liczbą parzystą. Prostokąty nie mogą zatem wypełnić kwadratu 9×9, gdyż 81 jest liczbą nieparzystą.
Każda z liczb w diagramie daje parzyste pola (7->6,10,12/5->4,6/3->2). Suma parzystych liczb jest parzysta a ma być nieparzysta=81=9*9.Więc zadanie nierozwiązalne.
Można z 3 w trzecim wierszu od dołu zrobić 4 i podział wygląda tak:
http://pokazywarka.pl/11ujn4/
Najtrudniejsze było „oczywiście nie zabierając się w ogóle za rozwiązywanie”.
I najpierw zrobiłem, ale jak już zrobiłem, to pomyślałem, jak można podejść do tego inaczej i chyba wiem:
Jeśli w rekuto występuje liczba nieparzysta to znaczy, że dotyczy obszaru, którego jeden bok ma długość parzystą, a drugi nieparzystą, a to znaczy, że pole takiego obszaru jest zawsze liczbą parzystą.
Na rysunku mamy same liczby nieparzyste, czyli wszystkie obszary, które opisują, mają powierzchnie parzyste.
A kwadrat jest rozmiarów 9×9, czyli jego powierzchnia jest liczbą nieparzystą – czyli nie ma rozwiązania, bo 81 nie może być sumą samych liczb parzystych.
Nazywając wiersze cyframi od 1 do 9, a kolumny literami od A do I, rozwiązywalność można uzyskać zmieniając „3” na D7 na „4” albo „5” na F7 na „6”.