Tylko tu
We wszystkich szkołach podstawowych lub średnich na świecie dzieci w wieku 10-12 lat rozwiązują na lekcjach matematyki następujące zadanie:
Znajdź dwie liczby, których suma równa jest X, a różnica Y.
Natomiast w żadnej szkole nie rozwiązuje się zadania:
Znajdź cztery liczby, wiedząc że suma dwóch z nich wynosi X, a różnica Y.
A w Łamiblogu można coś podobnego rozwiązać, jeśli… starczy cierpliwości.
Cztery spośród cyfr od 1 do 9 należy wpisać do kółek wokół każdego kwadratu, w którym podane są: największa suma i największa różnica dwóch z nich. Wszystkie te cztery cyfry nie muszą być różne, ale cztery cyfry w każdym rzędzie i w każdej kolumnie powinny być różne.
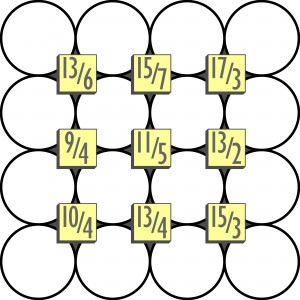

Komentarze
6789
5167
4356
2678
Nawet dość szybko mi to poszło. Zacząłem od prawego górnego rogu, bo tam musi być 8 i 9 oraz 6 i 7. Później jest prosto.
6789
5167
4356
2678
Górny wiersz aż się prosi o 6,7,8,9 🙂
6789
5167
4356
2678
Raczej proste; pół godziny na napisanie uniwersalnego solvera i sekunda jego pracy.
W zasadzie Łamiblog to nie Project Euler, ale cóż – można i tak…
mp
6789
5167
4356
2678
Zaczynamy od 17/3, będzie zestaw 6*89 (cyfry ułożone kolejno, więc brakującą będzie 6, 7 lub 8)
13/2, pasują tylko dwa zestawy: 5567, 5667, ale z 17/3 wynika, że będzie ten drugi, na dodatek w górnym wierszu będzie 6 i 7
Itd. idąc bardziej dołem szybko ograniczamy liczbę możliwości i zmierzamy do szczęśliwego zakończenia.
Bardzo przyjemnie się rozwiązywało, tak pyk, pyk, pyk 🙂
6789
5167
4356
2678
Bardzo przyjemne zadanie i w sumie całkiem proste. Wystarczyła chwila zastanowienia i kartka z ołówkiem. Całość zajęła ok. 5 minut 🙂
6789
5167
4356
2678
Co do Project Euler, to w Łamiblogu czasami pojawiają się zadania, które wymagają wsparcia komputera. Czasami napisanie dobrego programu, znajdującego w sensownym czasie rozwiązanie problemu, jest całkiem sporym wyzwaniem 🙂
Chciałem napisać program… ale jedyne, na co mi pozwoliła wiedza, to napisanie programu, który pokazał tylko możliwe kombinacje dla każdego kwadracika 2×2.
Udało mi się na piechotę obliczyć. Zacząć od prawych ósemek, później dziewiątka itd. Metodą prób i błędów zajęło mi to 9 plansz.
6789
5167
4356
2678
Pozdrawiam
6789
5167
4356
2678
Rozwiązuje się szybciutko od prawego górnego rogu. Wiadomo, że 17=8+9 i tylko tak.
Chwila zastanowienia i wiadomo, że pod spodem musi być 6,7 dokładnie w tej kolejność, natomiast pod 6 musi być 5. Po krótkiej chwili pęka prawa strona od góry do dołu i… reszta to formalność.
Komp by tutaj więcej przeszkadzał niż pomagał ale 5 minut to to nie było 😉
6789
5167
4356
2678
jedyne rozwiązanie !!!
6, 7, 8, 9
5, 1, 6, 7
4, 3, 5, 6
2, 6, 7, 8