Bez równań i ułamków
Tym razem będzie o pewnym wyróżniającym się oryginalnością rodzaju łamigłówki powstałym w ostatnich latach, który ma – jakżeby inaczej – japoński rodowód. Jego nazwę można przetłumaczyć jako labirynt pól, a autorem jest Naoki Inaba – bodaj najbardziej kreatywny wymyślacz diagramowych zadań logicznych.
Oto prosty przykład:
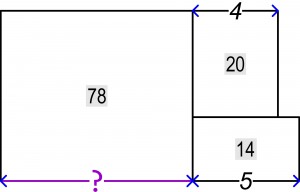
Liczby oznaczają długości boków i powierzchnie prostokątów; podstawowa jednostka jest oczywiście taka sama.
Właściwie rysunek wystarcza, aby zorientować się, o co chodzi – znak zapytania niby wszystko wyjaśnia, ale…
Kiedy przed paru laty zetknąłem się z takimi łamigłówkami, pomyślałem w pierwszej chwili, że ich niezwykłość jest jakimś nieporozumieniem. Przecież w tym konkretnym przypadku wystarczy jedno proste równanie:
?=78/(20/4+14/5)
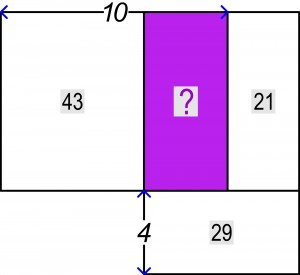
I drugi przykład:
Teraz trzeba określić wielkość powierzchni, czyli długości dwóch boków prostokąta – podstawy x i wysokości y , więc przyda się układ dwóch równań:
x=29/4-21/y
x=10-43/y
Niby w rozwiązaniach obu przykładów wszystko jest jak należy, ale z punktu widzenia „instrukcji obsługi” prawie wszystko jest źle, bowiem chodzi o coś innego: istota i cały urok łamigłówki polega nie tyle na znalezieniu rozwiązania, co sposobu rozwiązywania i to dość szczególnego. A mianowicie, sposób powinien być taki, aby nie zawierał równań, ani ułamków; korzystać wolno wyłącznie z liczb całkowitych oraz wzoru na pole prostokąta, a przede wszystkim z logiki, kombinowania i spostrzegawczości. Nie należy też sugerować się proporcjami na rysunku, bo nie muszą one odpowiadać rzeczywistym i z reguły nie odpowiadają.
Wróćmy do pierwszego przykładu.
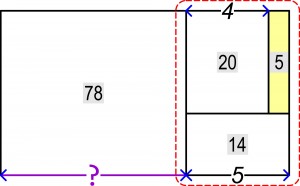
Zaczynamy od dopełnienia całości do prostokąta.
Dopełnienie ma wysokość 5 (20/4) i podstawę 1 (5-4), a zatem jego powierzchnia wynosi 5. Powierzchnia prostokąta obwiedzionego czerwoną linią równa jest 39 (20+5+14), a więc jest dwukrotnie mniejsza, niż sąsiedniego większego prostokąta (78) o takiej samej wysokości, a ponieważ podstawa (39) wynosi 5, więc podstawa (78) musi być dwukrotnie większa, czyli ?=10. Proste?
Kolej na drugi przykład (trudniejszy) rozwiązywany na dozwoloną modłę.
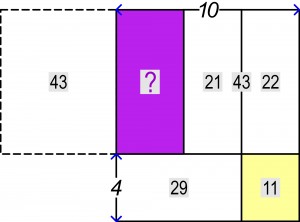
Przenosimy prostokąt (43) w prawo na drugą stronę (?) i dopełniamy całość do prostokąta. Prostokąt (43) pokryje częściowo (21), a pozostała jego część będzie prostokątem (22).
Dopełnienie ma powierzchnię 10×4-29=11. Nad nim znajduje się prostokąt o takiej samej podstawie i dwukrotnie większej powierzchni (22), a stąd wniosek, że łączna powierzchnia (21) i (?) jest dwukrotnie większa niż powierzchnia prostokąta (29), czyli wynosi 58. A zatem ?=58-21=37.
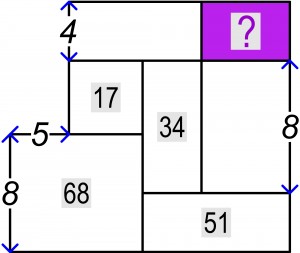
Czy po „treningu” poradzą sobie państwo z rozwiązaniem poniższego zadania? Obliczyć purpurową powierzchnię „po polsku” – prosta sprawa, rozwiązać zadanie „po japońsku” – nie tak łatwo, bo to dość twardy orzech.
Zdaję sobie sprawę, że rozwiązanie, które jest opisem rozwiązywania, to nie to samo, co podanie krótkiej odpowiedzi, więc z góry dziękuję wszystkim, którym starczy cierpliwości, aby takowym w komentarzu się pochwalić.

Komentarze
W zadaniu należy znaleźć pole prostokąta o wysokości 8, znajdującego się pod polem oznaczonym znakiem zapytania. A potem podzielić to pole na połowę, ponieważ szukany prostokąt ma taką samą podstawę oraz wysokość równą 4. Końcowy wynik to 25.
http://pokazywarka.pl/pxrmgb/
Zadanie proste.
8*5=40.
68-40=28
28-17=11 (lewo-dolny róg figur ’17’ i ’34)
Czyli pod ’11’ też jest ’17’ o wysokości prostokąta 51.
51=17*3
czyli na szerokości 51-dynki są trzy prostokąty ’28′(17+11)
3*28=84
84-34=50
‚?’ ma wysokość 4
czyli ?=50/2=25
Pole powierzchni purpurowego prostokąta=25. Spróbuję bez rysunku.
Odcinamy pionowo z lewej str. prostokąt o polu 8×5. Wtedy z lewej boki od góry to 4,h,8. odpowiednio z prawej od góry to 4,8,h.
Z 68 pozostało 28. Prawy jego bok przedłużamy w górę, aż przetnie pierwszy prostokąt. Lewa część tego prostokąta ma pole 14 ( podstawa taka jak u tego o polu 28, a wys. 2 razy mniejsza). Prawa część I prostokąta ma pole=17, bo pod nim jest prostokąt o polu=34 (podstawy równe wysokość jednego 4, drugiego 8). Teraz prostokąt o polu 28 dzielimy na dwa przedłużając górny bok prostokąta o polu 51 w lewo. Dolna część ma pole=17 , tak jak drugi od góry z lewej (podstawa taka sama i wys. równa h). Druga część 28-17=11. Dalej zauważamy, ze na dole są prostokąty o polach 17 i 51, wysokość mają jednakową, więc podstawa większego jest 3 razy większa od podstawy mniejszego. Pole purpurowego jest 2 razy mniejsze od tego pod nim. To większe ozn. P. Wtedy (34+P)/3=11+17, stąd P=50, a dalej pole purpurowego prostokąta=25
Nieco inny (krótszy) sposób rozwiązania drugiego przykładu:
skoro ’11’ ma wysokość 4
to ’22’ ma wysokość równą 8
prostokąt 8×10 wynosi 80
?=80-43=37
Orzech w istocie, jak na Łamibloga przystało, dość twardy.
Po zauważeniu, że wysokość prostokąta 17 i 51 jest jednakowa, wiemy, że podstawa 51 jest trzykrotnie dłuższa od 17 (bo 51=17*3).
Następnie prostokąt 68 dzielimy na dwa prostokąty o polach 40 (8*5) oraz 28 (68-40)
Rys. http://bankfotek.pl/view/1953931
W kolejnym etapie powstały prostokąt 28 dzielimy na dwa o polach 17 (wyżej wyjaśnione dlaczego) oraz 11 (28-17)
Powstaje nam duży zielony prostokąt o polu 62 (34+17+11) i wysokości 8 a więc powyżej niego niebieski prostokąt o wysokości 4 ma pole 31.
Rys. http://bankfotek.pl/view/1953932
Następnie przedłużamy górną podstawę prostokąta ’68’ otzrymując dwa prostokąto o polach trzykrotnie większych od ich sąsiadów po lewej, czyli 51 i 33 odpowiednio.
Rys. http://bankfotek.pl/view/1953936
Suma tych dwóch zielonych to 84 więc nowo obliczony niebieski prostokąt o wysokości 8 ma pole 50 (84-34) zatem znajdujący się nad nim szukany prostokąt o wysokości 4 ma pole 25.
Rys. http://bankfotek.pl/view/1953939
Mam nadzieje, że opis klarowny 🙂
podział: 68–8×5=28
spostrzeżenie: 51=17×3
makao: 3×28–34=50
rozwiązanie: 25
?=25
A teraz jak można do tego dojść:
Z lewego dolnego prostokąta odcinam 8*5 i zostaje prostokąt o powierzchni 68 – 40 = 28.
Teraz trzeba zauważyć, że prostokąt o powierzchni 17 i prostokąt o powierzchni 51 mają tą samą wysokość, czyli długość prostokąta „51” jest 3 razy większa niż „17”.
Stąd 3 * 28 = 34 + pole poniżej pytajnika, czyli pole pod pytajnikiem = 84 – 34 = 50.
A ponieważ pole poniżej pytajnika ma wysokość 8, a pole z pytajnikiem ma wysokość 4, to pole z pytajnikiem ma połowę jego powierzchni, czyli 25.
Strasznie trzeba się pilnować, żeby po japońsku nie użyć jakiegoś ułamka.
Szukane pole to 25.
Z prostokąta 68 odcinamy lewą część 5×8 o polu 40 – zostaje nam prostokąt o polu 28.
Prostokąty 17 i 28 zamieniamy miejscami.
Prostokąt ? podwajamy i przesuwamy w dół.
http://www.gg.pl/dysk/p6z7_ZWbVLVQpqz7_ZWbRJw/DSC_1465.jpg
Teraz dopiero zauważyłem, że w ostatnim kroku można wykonać jeszcze mniej obliczeń:
51 = 3 * 17, zatem
34 + 2 * ? = 3 * 28
34 + 2 * ? = 84
2 * ? = 50
? = 25
25
Można to rozwiązać w pamięci. Faktycznie ładne zadanie.
Wciągnęłam się! Więcej tego typu zadań znalazłam po wpisaniu w google grafika „Inaba puzzle”. Z tego, co widzę na jednym ze zdjęć, pan Inaba wydał też parę zbiorów zadań. Ale w Polsce tych zbiorów pewnie nie wydano? Na Amazonie też ich nie ma, a szkoda.
Rozrywka jest jednak niszowa i wydawcom się po prostu nie opłaca. W Japonii istnieje kilka małych wydawnictw, specjalizujących się w takich publikacjach i zainteresowanie jest większe, niż gdzie indziej, więc biznes jakoś się kręci. Parę zbiorków z „labiryntami pól” wydano tylko w Japonii.
mp
Bardzo fajne zadanie, chociaż trudniej opisać rozwiązanie niż rozwiązać, ale spróbuję. Mała legenda: L51 – długość prostokąta o polu 51, H? – wysokość szukanego prostokąta, PL51x8 – pole prostokąta w bokach L51 i 8.
P? =(4/8)x(PL51x8-34).
H17=H51, więc PL51x8=(51/17)xPL17x8=3x(68-5×8)=84
Stąd P?=1/2x(84-34)=25.
?=25.
Po japońsku: Oznaczmy powierzchnię szukanego prostokąta rzez X. Prostokąt pod nim ma powierzchnię 2X. Prostokąty 68 i 17 zamieniamy miejscami. Z prostokąta 68 odcinamy prostokąt 5*8=40 i zostaje z niego 28. Mamy proporcję (nie równanie 😉 ) (2X+34)/28=51/17 skąd X=25.
Po polsku: Poziomy bok prostokąta 17 oznaczmy przez b. Z równania (5+b)*8=68 wyliczamy b=7/2. Oznaczmy poziomy odcinek szukanego prostokąta przez a. Mamy a=3b-(5+b)/2=25/4. X=4*25/4=25.
Największą trudność w tym zadaniu sprawiło mi określenie co tak naprawdę wolno a czego nie wolno robić. Warunek „….bez równań….” jest jednak nieco mylący, gdyż następujący fragment rozwiązania drugiego przykładu:
„……Nad nim znajduje się prostokąt o takiej samej podstawie i dwukrotnie większej powierzchni (22), a stąd wniosek, że łączna powierzchnia (21) i (?) jest dwukrotnie większa niż powierzchnia prostokąta (29), czyli wynosi 58. A zatem ?=58-21=37….”
Jest po prostu opisem utworzenia i rozwiązania następującego równania:
(21+X)/29=22/11, skąd X=37.
A zatem równania możemy rozwiązywać ale przy dwóch warunkach.
1. Zmienną dozwolonego równania może być wyłącznie powierzchnia (a nie długość odcinka) .
2. Strony równania są stosunkami powierzchni o jednakowym ilorazie.
Chociaż tak naprawdę stwierdzenie, że odcinek ma długość 1 bo jest różnicą 5-4 to też rozwiązanie równania. Więc może ostatecznie taki jeden warunek: Wolno rozwiązywać równania pod warunkiem, że dają one tylko całkowite wyniki.
Ale wszak we wpisie stoi: „korzystać wolno wyłącznie z liczb całkowitych”.
mp
-Fioletowy ma o połowę mniejsze pole od prostokąta leżącego pod nim (jeden bok ten sam, drugi o długości 4 zamiast 8)
-Pole prostokąta leżącego bezpośrednio pod 17 z górnego lewego rogu wynosi 68 – 5*8 = 28
-Zatem pole prostokąta leżącego nad 51 będzie trzy razy większe (bo 51 = 3*17 i obydwa mają drugi bok o tej samej długości)
-Czyli pole prostokąta leżącego pod fioletowym wyniesie 3*28 – 34 = 50
-Zatem pole fioletowego to połowa z niego, czyli 25
Zadanie dobrą chwilę mi zajęło, ale ja słaby z geometrii jestem. Więc chyba jednak nie aż taki twardy orzech 🙂
Zgoda. Moje wątpliwości dotyczyły głównie zakazu stosowania równań. Próbowałem wykazać, że nie da się uniknąć ich stosowania. Tak czy inaczej łamigłówka jest bardzo fajna. Kojarzy się ze sztuką konstruowania figur cyrklem i linijką. 🙂
o rany, ale zamotałem, faktycznie po podziale 68 na 40+28 i zamianie miejscami powstałego 28 z leżącym nad nim 17 zadanie robi się trywialne
Można zaproponować drobną kontynuację? Tu jest kilka przykładów przestrzennych: http://pokazywarka.pl/fg5tp9/ Umiem rozwiązać tylko pierwszy. Czy ktoś podpowie rozwiązania pozostałych trzech?
@OlaGM: 24, 32, 21, 52
w drugim wartosci 15 i 29 są niepotrzebne.
Wiąz, dziękuję 🙂 A jakie rozumowanie trzeba przeprowadzić w przykładach 3. i 4?
@OlaGM:
3. ’14’-ki maja jeden bok tej samej długości, a więc muszą mieć tą samą szerokość (rowne pola), a więc tak samo jest z 15 (styczne bokiem do 14), wniosek: obie 15-ki są takie same: bok=6, czyli ?=6*6 -15
4.
17 to 34/2 => szerokość 34-ki=5
czyli szerokość ‚?’=10-5=5
17-ka dzieli wysokość na 2 czyli wysokosc 26 i 17 równe,
skoro szerokość ? i 34 jest ta sama, to ?=2*26=52
Mam dwie wątpliwości:
a) Skąd wiesz, że szerokość 34-ki to 5?
b) Skąd wiesz, że 17-ka dzieli wysokość na połowę?
Czy to jakoś wynika z rysunku (ja tego nie umiem zobaczyć…)
Jeśli dobierze się inne dane (34-ka ma wymiary 17×2, a 17-ka ma wymiary 17×1), to w konsekwencji 26-ka ma wymiary (5-1) x 6,5, z kolei [?] ma wymiary (10-2) x 6,5, czyli też wychodzi 52.
Czy to nie jest tak, że założenia a) i b) nie mają znaczenia, że [?] zawsze będzie 2 x większe niż 26?
a) 34 i 17 maja wspólny bok o tej samej dlugosci, a wiec…. 🙂 jesli pole jest dwa razy wieksze to drugi bok musi być jaki?
b) patrz punkt a).
a i b maja znaczenie, bo inaczej nie wiedzielibysmy ile odjąc od 10 zeby otzrymac szerokosc ‚?’
Aaaaa zrozumiałem, o co ci chodzi… ja to widze inaczej, to znaczy od razu widzę skalę, jeśli o tyle samo zmieni sie wysokość 17’ki, to o tyle samo zwiększy się szerokość ‚?’ a co za tym idzie, wysokość 26’ki i stosunki pozostana te same, prawie jakw Talesie. Ja przyjąłem stosunek 34/17, czyli 2, można przyjąć x, które się skróci.
P.S. rozwiązanie byłoby deczko trudniejsze gdyby 10/5 było nierówne 34/17 (ale to tylko skala), a jeśli stosunki są równe to widać od razu zależność.
Jest tak, jak piszesz OlaGM. Jak narysujemy przekątną trójkąta o znanych bokach 5 i 10 to zupełnie przypadkiem uzyskamy jeszcze dwa małe trójkąty podobne (17/34=5/10) i w związku z tym ? jest 2 x większe od 26.
Bardzo dziękuję za tę dyskusję 🙂
Obawiam, że 4. przykład jest dla mnie za trudny… Umiem go rozwiązać tylko w ten sposób, że przyjmę jakieś konkretne liczby i sprawdzę, co w konsekwencji otrzymam jako [?]. Z o b a c z y ć tego nie umiem, trudno 🙂
Pytałam w sklepie japońskim, czy sprowadziliby te książeczki („Menseki Meiro”) do Polski. Okazało się, że tak, z tym że kosztowałyby po 45 zł od sztuki. Jeśli ktoś chce, mogę podać namiar na ten sklep.
(a na Amazonie są w cenie 8-12 funtów)
OlaGM, możesz 4. przykład tak:
Pionowy bok „17” oznaczyć a. Wtedy odpowiedni bok „34” wynosi 2a.
Reszta boku długości 5 wynosi 5-a. Drugi ,mniejszy, prostokąt z przodu ma boki : krótszy równy 5-a, dłuższy równy 10-2a.
Teraz rozumiem. Szary prostokąt z bokiem (10-2a) ma dwa razy większe pole niż prostokąt z bokiem (5-a) bez względu na to, ile wynosi ich wspólny bok. Dziękuję, Logi 🙂