Sumowo
Jeśli, zaczynając od jedynki w wierzchołku trójkąta, który ma także dwa „jedynkowe” boki (podstawy na razie brak), pod każdą parą liczb będziemy wpisywać ich sumę, to powstanie trójkąt Pascala. Gdy sumy pojawiają się nad parami liczb, zaczynając od liczbowej podstawy, wówczas powstaje trójkąt modularny – o ile każda suma będzie zapisana modulo x. Gdybyśmy pominęli modulo, to utworzony trójkąt można by nazwać sumowym. To określenie trochę razi. Przymiotniki różnicowy i iloczynowy są przyswojone, a sumowy jest jak growy (od gra), czyli aż się prosi, żeby go omijać. Mimo to zaryzykuję próbę oswojenia.
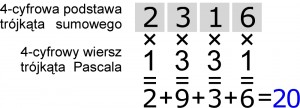
Trójkąt sumowy jest „przewidywalny” w tym sensie, że znając wartości i kolejność liczb w podstawie, łatwo określić, jaka znajdzie się w wierzchołku. Wystarczy wpisać pod podstawą wiersz takiej samej długości z trójkąta Pascala. Mnożąc następnie odpowiadające sobie liczby, a potem dodając iloczyny, otrzymamy liczbę w wierzchołku. Na przykład:
Łatwo ustalić, dlaczego tak będzie, znając sposób tworzenia trójkąta Pascala. Na tym także zasadza się sekret sztuki z wpisu Według Pascala – co wyjaśnili Państwo w komentarzach – tylko że liczby zapisuje się zawsze modulo 9, więc działania są prostsze.
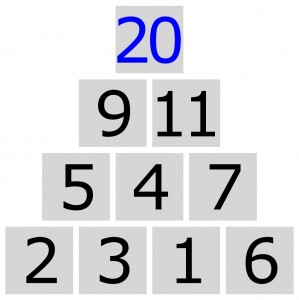
A oto cały trójkąt wsparty na powyższej podstawie:
To unikat (już nie, bo „unikaty” są trzy – p. komentarz Andrzeja) wśród trójkątów sumowych czwartego rzędu (4-cyfrowa podstawa), ze względu na dwie własności:
– wszystkie liczby są różne,
– liczba w wierzchołku jest najmniejszą z możliwych.
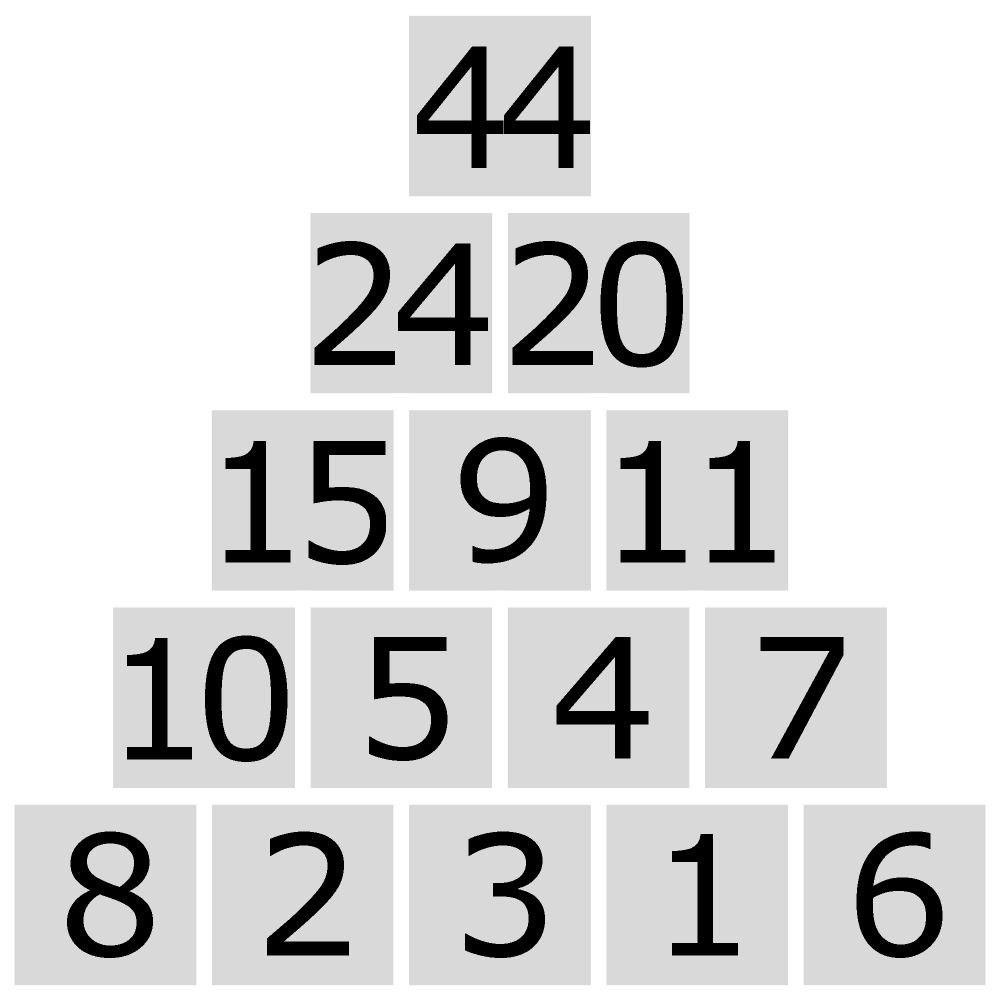
Nie znam w miarę prostego, logicznego sposobu szukania trójkątów sumowych wyższych rzędów, spełniających oba podane warunki. Nie wiem nawet, czy ktoś ich szukał, korzystając z programu komputerowego. Zapewne nie jest to proste, skoro – gdy zadanie polegające na szukaniu takiego trójkąta piątego rzędu pojawiło się przed dziesięciu laty w konkursie matematycznym – jego autor miał przygotowane następujące rozwiązanie:
Łatwo zauważyć, że stanowi ono rozwinięcie przedstawionego wyżej trójkąta czwartego rzędu – dodany jest lewy bok. Tymczasem uczestnicy konkursu znaleźli lepsze rozwiązanie, czyli z mniejszą liczbą w wierzchołku. Jakie?
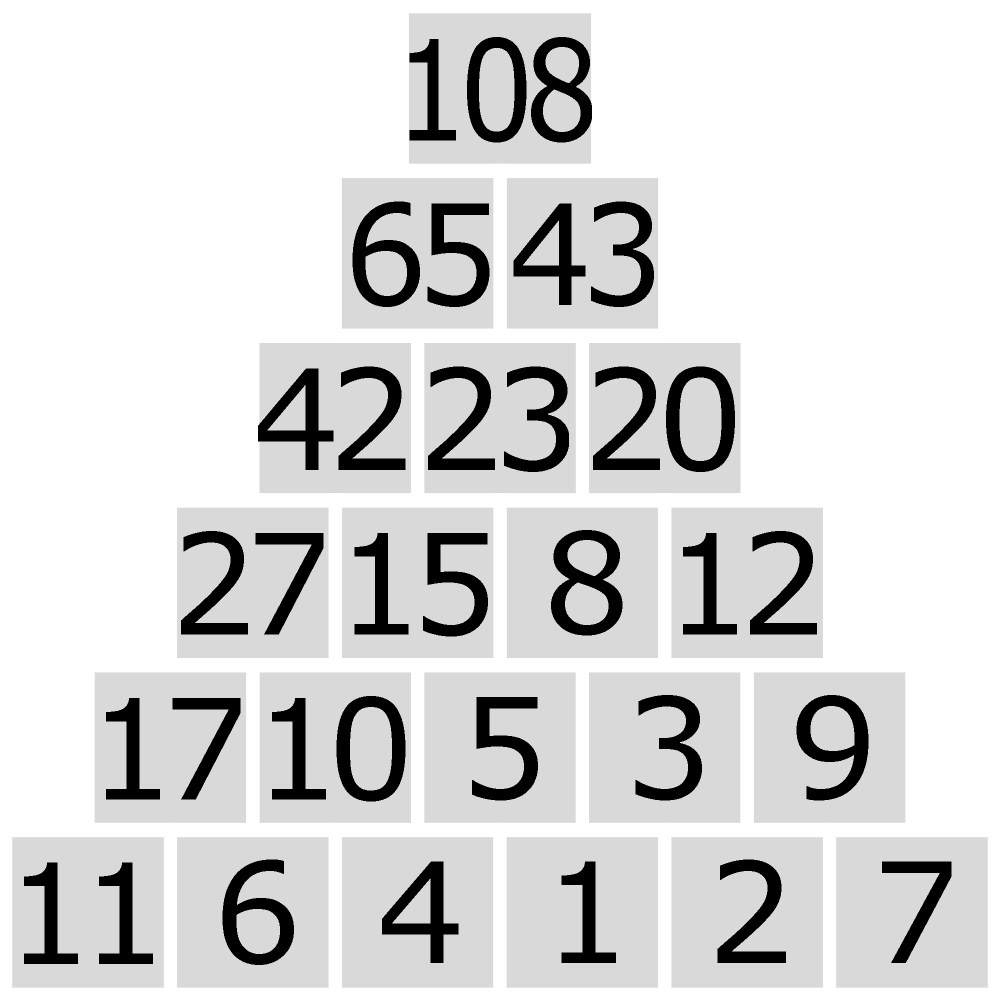
A może ktoś pokusi się o znalezienie najlepszego rozwiązania dla trójkąta szóstego rzędu. Poniższe na pewno nim nie jest.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.

Komentarze
43
20, 23
12, 8, 15
9, 3, 5, 10
7, 2, 1, 4, 6
To akurat nie było trudne. Chyba, że jest lepsze rozwiązanie.
Ale reszta? Rzeczywiście, reszta nie nastraja optymistycznie.
Pozdrawiam
Naturalną konsekwencją poprzedniego rozwiązania jest:
102
59, 43
39, 20, 23
27, 12, 8, 15
18, 9, 3, 5, 10
11, 7, 2, 1, 4, 6
Ale czy to jest najlepsze? trudno powiedzieć.
Pozdrawiam
Nieco manipulując przy poprzednim rozwiązaniu uzyskałem:
101
54, 47
34, 20, 27
22, 12, 8, 19
13, 9, 3, 5, 14
6, 7, 2, 1, 4, 10
Kto da mniej?
Pozdrawiam
Dla piątego rzędu znalazłam taki trójkąt
43
20 23
12 8 15
9 3 5 10
7 2 1 4 6
A dla szóstego:
98
52 46
32 20 26
21 11 9 17
14 7 4 5 12
8 6 1 3 2 10
Znakomitym ułatwieniem jest podpowiedziane powiązanie z trójkątem Pascala
100
44, 56
24, 20, 36
15, 9, 11, 25
10, 5, 4, 7, 18
8, 2, 3, 1, 6, 12
Kto da mniej 😉
43
20, 23
12, 8, 15
9, 3, 5, 10
7, 2, 1, 4, 6
a co do trójkata piatego rzedu to bedzie rozwiazanie chyba
Mniejszy trójkąt
43
23,20
15,8,12
10,5,3,9
6,4,1,2,7
Większy
98
52,46
32,20,26
21,11,9,17
14,7,4,5,12
8,6,1,3,2,10
Jeszcze większy
212
102, 110
59,43,67
39,20,23,44
27,12,8,15,29
18,9,3,5,10,19
11,7,2,1,4,6,13
Jak zbuduję większy to napiszę.
Prawidłowym (w sensie optymalności) rozwiązaniem jest 6.4.1.2.7. Rozwiązania należy szukać w problemie sformułowanym dla trójkąta szóstego rzędu 🙂
Natomiast rozwiązaniem trójkąta szóstego rzędu jest 8.6.1.3.2.10 o sumie 98, choć istnieje jeszcze rozwiązanie ‚pośrednie’ o sumie 101 dla 10.4.1.2.7.6. Oczywiście ilości rozwiązań można pomnożyć przez 2, ze względu na oczywistą symetrię.
To i ja sie dolacze:
………….98
……….52..46
……..32..20..26
……21..11…9..17
….14…7…4…5..12
…8…6…1…3…2..10
Wydaje mi sie, ze powinno sie osobno rozpatrywac parzyste i nieparzyste ilosci liczby w podstawie. Tzn. jezeli dla 4 liczb mamy 2,3,1,6 to aby zrobic trojkat dla 6 liczb, trzeba ulozyc go tak, aby dodac na poczatku i na koncu podstawy(4) najmniejsze liczby nie wystepujace w trojkacie(4). Sa to liczby 8 i 10. Stad trojkat dla 4.
Postepujac podobnie mozna znalezc dobry trojkat dla 5 liczb. Otoz dla trzech optymalna podstawa jest: 2,1,4. W trojkacie tak stworzonym najmniejsze liczby tam nie wystepujace to 6 i 7. Wykorzystujac to mozna zrobic trojkat(5), ktorego podstawa bedzie 6, 4, 1, 2, 7. Widac, ze na koncach mamy 6 i 7, a w srodku podstawe(3) od konca. Ten trojkat wyglada tak:
………43
……23..20
….15..8…12
..10..5..3….9
6…4…1…2…7
Liczba na wierzcholku jest o jeden mniejsza niz w tekscie Pana Marka.
Analogicznie dla trojkata z 7 liczb mozna szukamy brakujacych w trojkacie(5). Sa to 11 i 13. Zapisujemy je na koncu, a w srodku uzupelniamy podstawa(5) w odwrotnej kolejnosci. Podstawa(7) bedzie nastepujaca: 11, 7, 2, 1, 4, 6, 13. Na gorze bedzie wtedy 212.
Napisalem program na komputerze, ktory sprawdza wszystkie mozliwosci, i doszedlem do reguly w czasie sprawdzania trojkata o podstawie 7. Na calkiem dobrym komputerze sprawdzenie wszystkich mozliwosci zajelo 4 godziny;).
Takze nie podejme sie sprawdzac tego przepisu dla 8 liczb w podstawie…
Pozdrowienia
ps. nie wiem, dlaczego nie zgadza sie to dla przejscia z optymalnej podstawy(2): 1,2 do optymalnej podstawy(4): 2,3,1,6.
Pobawiłam się trochę wyższymi rzędami. Ponieważ nie potrafię programowac, nie jestem do końca pewna, czy wyniki są optymalne.
Mój sposób opiera się na uwadze autora, że liczba w wierzchołku to suma iloczynów liczb w podstawie i odpowiednich liczb w odpowiednim wierszu trójkąta Pascala. A ponieważ każdy wiersz trójkąta Pascala ma największe liczby w środku wiersza, zaś maleją ku brzegom, więc należy w środku podstawy umieszczac jak najmniejsze liczby – najlepiej 1 i 2.
Nim wiersz rozbudowałam, uzupełniałam, co możliwe, w górę i dopiero wtedy najmniejszą z „wolnych” liczb dopisywałam do już zapisanych. I znów uzupełniłam górne wiersze, potem rozszerzyłam dół. Zdarzało się oczywiście, że nagle jakaś liczba się dublowała, wtedy nieraz wystarczyło zamienic nowo wpisywane liczby miejscami, a czasami trochę inaczej wybrać.
Tym sposobem znalazłam trójkąty dla t=28 i t = 36.
Pierwszy zajął mi dokładnie 17 min, drugi tylko trochę więcej. Czy ktoś, z wsparciem komputerowym, może orzec, czy to optimum?
I tak:
t=28
(… areszt tymczasowy:) mp
t=36
484
269 215
167 102 113
108 59 43 70
69 39 20 23 47
42 27 12 8 15 32
24 18 9 3 5 10 22
13 11 7 2 1 4 6 16
Pozdrawiam
Anka
Największy, ale tu nie mam 100% pewności co do mimimalności sumy.
504
podstawa
9,14,2,4,1,7,3,12
lub
12,9,4,2,3,7,1,16
Pozdrowienia
Następny unikat wśród trójkątów sumowych czwartego rzędu:
7, 2, 1, 4.
Dla ósmego rzędu:
(… areszt tymczasowy:))
W takim razie pozwolę sobie dopisać trzeci unikat:
7, 1, 2, 4
mp
Pan, Panie Marku, potrafi zmobilizować do pracy. Tak to jest, jak się nie postępuje metodycznie. Może tym razem to już to.
98
52, 46
32, 20, 26
21, 11, 9, 17
14, 7, 4, 5, 12
8, 6, 1, 3, 2, 10
Pozdrawiam
Polak potrafi:)
mp
Niestety, dla t=36 podana przeze mnie końcowa suma jest mocno przesadzona 🙂
Wypychając ze środka 2-kę i wstawiając 3-kę, byłam w stanie na pozostałych „tłustych” miejscach ulokowac mniejsze liczby:
16, 8, 6, 1, 3, 2, 10, 15
by ostatecznie otrzymać w sumie 465.
Zadanie na tyle mnie zaintrygowało, że jeszcze przymierzyłam się do t=45.
Stanęło na ciągu
21, 11, 7, 2, 1, 4, 6, 13, 17
bądź
17, 11, 7, 2, 1, 4, 6, 13, 21
Obydwa z sumą 1000.
Że wszystkie liczby trójkąta są różne, łatwo sprawdzić, ale czy to minimum? Chcę wierzyć, że tak.
Anka
Trójkąt ósmego rzędu
suma 465
podstawa
15,10,2,3,1,6,8,16.
Tak to pośpiech ludzi gubi.
Pierwsze przymiarki.
7 2 1 4 6 – suma 43
n = 6
10 2 3 1 6 8 – suma 98
n = 7
14 7 2 1 4 6 16 – suma 218
n = 8
15 10 4 1 2 7 6 11 – suma 474
Wedlug mnie piramida(8) wyglada nastepujaco:
………….465
……….241.224
……..143.98.126
…….91..52..46..80
……59..32.20.26..54
….38..21.11..9..17..37
..24..14..7…4…5..12..25
16…8…6…1…3…2..10..15
Nie sprawdzilem wszystkich mozliwosci, ale ta jest calkiem prawdopodobna.
pozdr
Dla trojkata 7-go rzedu na pewno nie przeskoczy sie 212, a podstawa bedzie taka:
11 7 2 1 4 6 13
Dla osmego rzedu prace trwaja…
a