Nie tylko iloczyny
We wpisie z 9 marca znalazło się następujące zadanie, pochodzące z tureckiego kwartalnika Akil oyunlari:
Zgodnie z oryginalnym objaśnieniem celem jest wpisanie w pola cyfr od 1 do 5 tak, aby w każdym rzędzie i w każdej kolumnie były różne cyfry. Klucz do rozwiązania stanowią liczby w kółkach – każda jest iloczynem czterech cyfr, które powinny znaleźć się w polach otaczających dane kółko.
Jak wynika z Państwa komentarzy, informacji w tym zadaniu jest o wiele więcej niż potrzeba do jednoznacznego rozwiązania, bowiem pozostanie ono jednoznaczne nawet po usunięciu dwunastu iloczynów. W dodatku programiści cpp i miodziu ustalili, że cztery pozostawione iloczyny mogą być rozmieszczone na 46 sposobów. Jakby tego było mało, Michał doszedł do oryginalnego wniosku, że przy ujawnionych wszystkich iloczynach nie jest potrzebna informacja, aby cyfry w rzędach i kolumnach były różne, bo i tak nie różne być nie mogą.
Chyba pierwszy raz spotkałem się w zadaniu zamieszczonym w fachowym piśmie z tak gigantyczną porcją zbędnej informacji. Trudno oprzeć się wrażeniu, że redagujący postąpili świadomie – im więcej podpowiedzi, tym prostsze zadanie, a ponadto przy ujawnieniu wszystkich iloczynów nie jest wyraźnie wskazane miejsce startu. Zabawę można zacząć właściwie gdziekolwiek i zmierzać do celu dowolnie wybraną drogą. Niech żyje wolność!
Przyszło mi do głowy, że w kółkach można umieszczać nie tylko iloczyny, ale także sumy czterech sąsiednich cyfr. Przy składnikach możliwości jest więcej, niż przy czynnikach, więc i kółek z liczbami trzeba wstawić nieco więcej. Aby jednak nie było zbyt prosto, poniższe zadanie jest mieszanką, czyli każda liczba może być zarówno sumą, jak i iloczynem – która czym, to także zagadka.
Wypada jeszcze dodać, że jest więcej niż jedna suma i iloczynów takoż powyżej jednego.

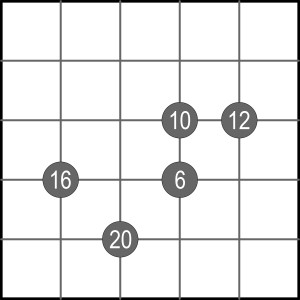

Komentarze
Bardzo fajne zadanko. Po chwili zastanowienia ciągle nie widzę sposobu na ładne rozwiązanie na piechotę (ładne tzn. takie, które nie będzie generowało zbyt dużo przypadków do rozważenia). Ale mam dwa pomysły, które mogą prowadzić do ładnego rozwiązania, ale czy tak rzeczywiście jest okaże się po głębszym zastanowieniu 😉
5 2 3 4 1
1 3 5 2 4
3 4 2 1 5
4 5 1 3 2
2 1 4 5 3
Jeżeli nie byłoby warunku o ilości mnożeń i dodawań to są inne rozwiązania
3 2 4 5 1
1 5 3 4 2
4 3 2 1 5
5 4 1 2 3
2 1 5 3 4
13452
52341
45213
34125
21534
Miodziu,
Widać, gdzie musi być iloczyn, a gdzie 2 sumy (czyli znowu mamy nieco za dużo informacji, ale przynajmniej podano ją w formie niedyskryminującej żadnej operacji). Jedyne, co musiałem zgadnąć, to czy w pewnym miejscu jest suma czy iloczyn. Potem „samo się robi”.
PS. Na szczęście skasowałem swój poprzedni program, na piechotę było szybciej.
Zagadką jest, co można zrobić z zadaniem, aby odpowiedź była jedna.
Właśnie. Chyba wystarczyłby warunek, że iloczynów jest więcej niż jeden.
mp
13452
52341
45213
34125
21534
jeżeli założymy, że można użyć dokładnie jednego iloczynu, to otrzymujemy rozwiązanie (jedyne przy tym założeniu):
32451
15342
43215
54123
21534
Warunek mówiący, że iloczynów jest więcej niż jeden nie poprawia sytuacji, a może nawet ją pogarsza. Nadal otrzymujemy więcej niż jedną odpowiedź. Aby uzyskać jednoznaczność rozwiązania trzeba coś z zadaniem jeszcze zrobić. Można spróbować przestawić kółka, można kółka dołożyć, itp.
Ja zdecydowałem się na nałożenie na zadanie następującego dodatkowego warunku: suma liczb leżących na przekątnych diagramu jest liczbą pierwszą.
Nie lubię takich „wydumanych” warunków. Zdecydowanie lepszy, bo bardziej związany z treścią zadania, byłby warunek niejako przeciwny do tego, który podałem poprzednio, czyli: iloczyn jest dokładnie jeden. Wtedy rozwiązanie jest jedno, ale zadanie staje się zbyt proste.
mp
Drugie rozwiązanie:
52341
13524
34215
45132
21453
spełnia warunki zadania (2 iloczyny, 3 dodawania)
Nie ma innych rozwiązań, nawet jeżeli zniesiemy warunek na liczbę sum i iloczynów.
Tzn. nie ma innych rozwiązań niż te 3 podane przeze mnie powyżej.
Na piechotę nie jest zbyt strasznie.
Od góry do dołu, od lewej do prawej, liczby przylegające do kółek:
341
45213
34125
15.
Pozdrawiam.
Teraz już rozumiem jaka powinna być odpowiedź:
32451
15342
43215
54123
21534
PS Ten tzw. „wydumany” warunek był tylko na mój własny użytek. Brzydki, ale skuteczny.
Umiejętność programowania przy rozwiązywaniu łamigłówek z jednej strony jest błogosławieństwem, z drugiej wielkim przekleństwem.
Błogosławieństwem, bo dzięki temu można zweryfikować czy łamigłówka jest jednoznaczna albo, tak jak to było w przykładzie sprzed kilki dni, pozwala znaleźć wszystkie możliwe układy danych wejściowych spełniających pewne reguły (nie wyobrażam sobie bowiem, że ktokolwiek byłby w stanie na piechotę odnaleźć te 46 układów czterech iloczynów oraz jednocześnie udowodnić, że żaden układ 3 iloczynów jest niepoprawny).
Przekleństwem, bo rozwiązanie aktualnego zadania z pomocą komputera jest bardzo proste, w zasadzie nawet nie trzeba myśleć przy pisaniu programu tylko wystarczy go napisać i przy odrobinie wprawy programistycznej program od razu będzie dobry. A takie podejście kusi człowieka, aby nie próbować rozwiązać zadania na piechotę.
Kolejną sprawą jest czas… Aby pomyśleć nad rozwiązaniem na piechotę potrzebna jest chwila spokoju, z kartką i ołówkiem (bo niewielu jest takich, którzy potrafią sobie to wszystko wyobrazić bez zapisywania) i nigdy nie wiadomo jak dużo tego czasu jest potrzebne. Natomiast program można napisać w krótką chwilę i nawet jeśli jego wykonanie będzie trwało godzinami, to wcale nie musimy przy tym być, komputer pracuje za nas i nie narzeka, że to długo trwa. Potem wystarczy krótka chwila na sprawdzenie wyników pracy i mamy gotowe rozwiązanie.
Tylko czy takie programistyczne rozwiązywanie zadań sprawia przyjemność? Bardzo rzadko 🙁
To jak uzasadnić sens istnienia Project Euler?
mp
Drugie rozwiązanie:
52341
13524
34215
45132
21453
Komentarz do zadania.
Ponieważ największą liczbą w kratkach jest 5, 20 musi być iloczynem.
6 może być iloczynem 1*1*2*3 lub sumą 1+1+2+2 – w każdym przypadku sąsiadują z nią dwie jedynki po przekątnej. Stąd wynika, że 16 jest sumą (gdyby była iloczynem, to tylko 1*1*4*4, więc w rozkładzie miałaby dwie jedynki, co kłóci się z tym, co już wiemy o 6).
Gdyby 10 była iloczynem, to byłby on postaci 1*1*2*5. To kłóci się z jedynkami obok 6. Czyli 10 jest sumą.
Jeżeli *założymy*, że 6 jest sumą, to 12 musi być drugim iloczynem.
Mając te informacje, łatwo rozwiązać zadanie na piechotę.
Ech… Użyłem nietrafnego słowa w puencie i wyszło inaczej niż zamierzałem. Powinno być:
„Tylko czy takie programistyczne rozwiązywanie łamigłówek sprawia przyjemność? Bardzo rzadko :-(”
Nie mam nic przeciwko wspieraniu się komputerem przy rozwiązywaniu zadań. Ba, lubię to i muszę przyznać, że jest wiele bardzo ciekawych problemów z ładnymi rozwiązaniami programistycznymi.
Jednak łamigłówka – jak sama nazwa wskazuje – powinna być zadaniem dla umysłu ludzkiego i tylko taki sposób rozwiązania uznaję za słuszny.
A Project Euler? Bardzo ciekawy zbiór zadań matematyczno/programistycznych. Ale do łamigłówek im daleko… 😉
A jeśli już mówimy o zadaniach matematycznych/programistycznych/łamigłówkowych, to chciałbym podzielić się z Panem zadaniem, które umieściłem w jednym z serwisów z zadaniami PROGRAMISTYCZNYMI, choć rozwiązanie wzorcowe jest czysto MATEMATYCZNE, licząc, że może po drobnej obróbce uda się Panu zainteresować nim wytrawnych GŁOWOŁAMACZY 😉
Treść po angielsku, ale zakładam, że to nie jest żaden kłopot: http://www.spoj.com/problems/MMMAGIC3/