Dominka
Robię korektę Omnibusa wakacyjnego, który trafi do kiosków pod koniec czerwca i przy okazji rozwiązuję po raz kolejny, dla świętego spokoju, niektóre z zamieszczonych w nim zadań logicznych. Są wśród nich takie, które układa się niełatwo i są takie, które niemal układają się same. Co ciekawe, te drugie bywają często atrakcyjniejsze i silniejsze logicznie od tych pierwszych. Należą do nich na przykład łamigłówki, które nazywam dominkami. To dodawania układane z kamieni domina dziewiątkowego, czyli z par cyfr od 0-0 do 9-9. Właściwie wystarczy napisać dodawanie, podzielić je na kamienie, a potem oddzielić kamienie od „szkieletu” i zadanie gotowe.
Celem jest oczywiście o odtworzenie działania.
Takie zadanie trzeba jednak jeszcze „uszlachetnić”, czyli dopracować tak, aby było logiczne, a nie polegało tylko na żmudnym sprawdzaniu wielu konfiguracji. Ściślej, chodzi o to, aby stworzyć możliwość dotarcia do celu na logikę, ewentualnie z niewielkim błądzeniem.
Logika dominki wynika z połączenia geometrii układu z arytmetyką. Aby zadziałała wypada jeszcze to i owo dodać w instrukcji:
– kamieni nie należy obracać – powinny znaleźć się w działaniu w takiej pozycji, jak na rysunku;
– niektóre cyfry (w poniższym zadaniu dwie) są ujawnione.
Jak wygląda dodawanie?
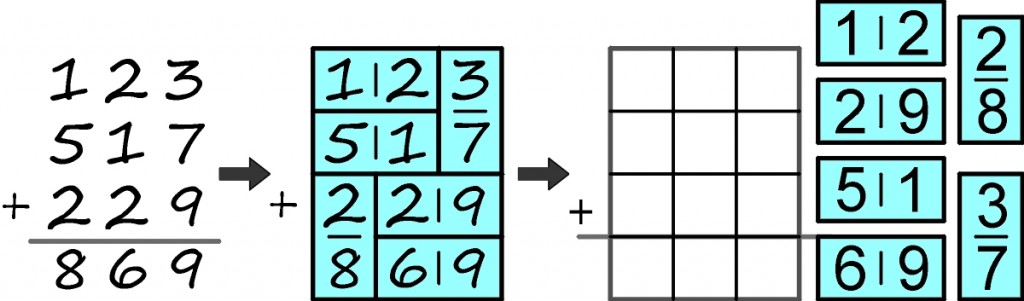


Komentarze
Dodawanie może wyglądać różnie:
2532+1225+1714=5471 albo 2222+1535+1714=5471. Czy to jedyne dwa możliwe rozwiązania – nie wiem. Może się zdarzyć, że niekoniecznie…
Pozdrawiam
2222+1535+1714=5471
Dodawanie wygląda ładnie.
2222
1535
1714
——
5471
2532
1225
1714
5471 albo
2222
1535
1714
5471
2222
1535
+1714
=5471
wesołe łatwe zadanko w sam raz do „porannej” kawki 🙂
Rozwiazuje sie przyjemnie – pol na logike, pol na proby. Ale sa dwa rozwiazania, bo dwa kamienie mozna zamieniac miejscami:
2222 (2532) + 1535 (1225) + 1714 = 5471
a
Dodawanie wygląda różnie, a dwa różne wyniki to x i y, gdzie
x+y=10825
x-y=117
Dodawanie wygląda tak:
2(22)2
1(71)5
+ 1 41 7
————
5354
wartości w nawiasach można zamienić miejscami.
Pozdrawiam
2532
1225
1714
—–
5471
lub 2222+1535+1714=5471
Pytanie: czy da się ułożyć takie zadanie, żeby było jedno rozwiązanie?
Oczywiście da się odpowiednio stawiając „gratisowe” cyfry.
Np. (pozwoliłem sobie delikatnie pomieszać oryginał)
http://i43.tinypic.com/2r3y05h.jpg
Jestem jednak przekonany, że nie da się tego zrobić bez dodatkowych (startowych) cyfr.
—–
Uwaga – nudy:
—–
a) „nad kreską” nie może być kwadratu 2×2 złożonego z kostek poziomych;
b) ani prostokąta 3×2 złożonego z jednej poziomej i dwóch pionowych.
Jedyny układ (dla 4×4) spełniający te warunki składa się z samych kostek pionowych -> dla którego możemy zamienić kolumny:
a) każda kolumna przekazuje +1/0 i/lub przyjmuje +1/0 (czyli jest opisywana przez dwie cyfry 0/1; 0/1)
b) jeśli są dwie kolumny o tym samym kodzie, to możemy je zamienić
c) jeśli wszystkie 4 kolumny mają różne kody, to i tak są dwa różne ustawienia dające dwa rozwiązania.
wg mnie powinno byc tak:
2222
1715
1417
5354
2222 + 1715 + 1417 = 5354,
2712 + 1225 + 1417 = 5354,
2222 + 1535 + 1714 = 5471
albo 2532 + 1225 + 1714 = 5471.