Pięć drzew
Ułożyć zadanie i nie potrafić go rozwiązać. Tak czasem bywa, ale częściej zdarza mi się znajdywać rozwiązanie, które – jak się później okazuje – albo nie jest najlepsze, albo nie jedyne. Co ciekawe, konsultanci też czasem zawodzą i dopiero niektórzy czytelnicy wyłapują potknięcia. Ostatnio taki przypadek miał miejsce w marcowym Świecie Nauki.
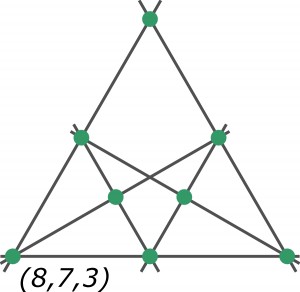
Artykuł nawiązywał do tzw. problemu sadzenia drzew, który w ogólnym ujęciu polega na posadzeniu n drzew w r rzędach tak, aby w każdym rzędzie rosło dokładnie k drzew. Bardziej konkretnie, chodzi o znalezienie maksymalnego r dla ustalonych n i k. Na przykład, jeśli n = 8 i k = 3, to rzędów r może być najwyżej 7, a drzewa należy posadzić tak:
Jedno z zadań konkursowych było nieco zakręcone, bo drzewa znajdowały się w węzłach siatki kwadratowej, a ponadto występowały dwie wartości r i k.
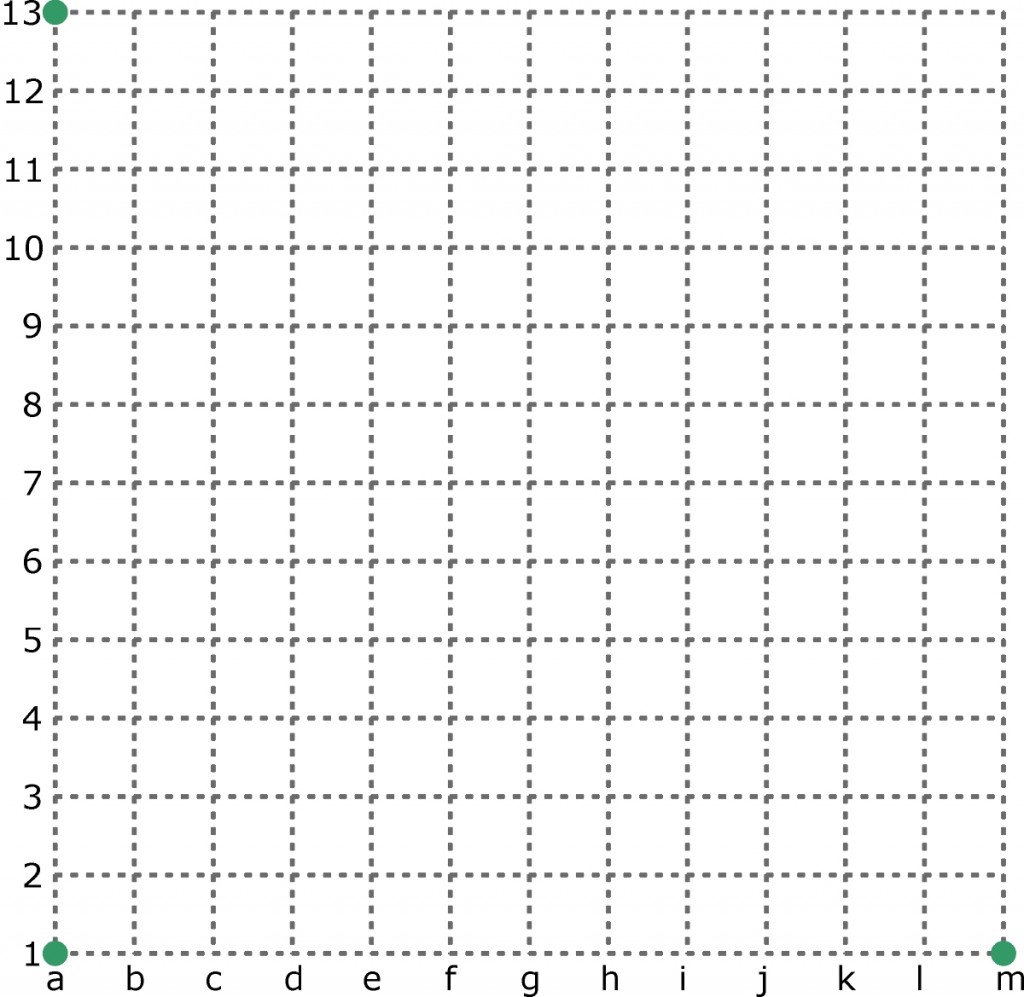
W sadzie rośnie 169 drzew. Na rysunku odpowiadają im węzły siatki kwadratowej. Osiem drzew przeznaczono do wykarczowania – trzy z nich (oznaczone na rysunku) znajdują się w rogach sadu, czyli w punktach a1, a13 i m1. Gdzie rośnie pięć pozostałych, jeśli wszystkie osiem tworzy siedem rzędów: sześć rzędów po trzy drzewa w każdym (nie więcej) oraz jeden rząd z czterema drzewami?
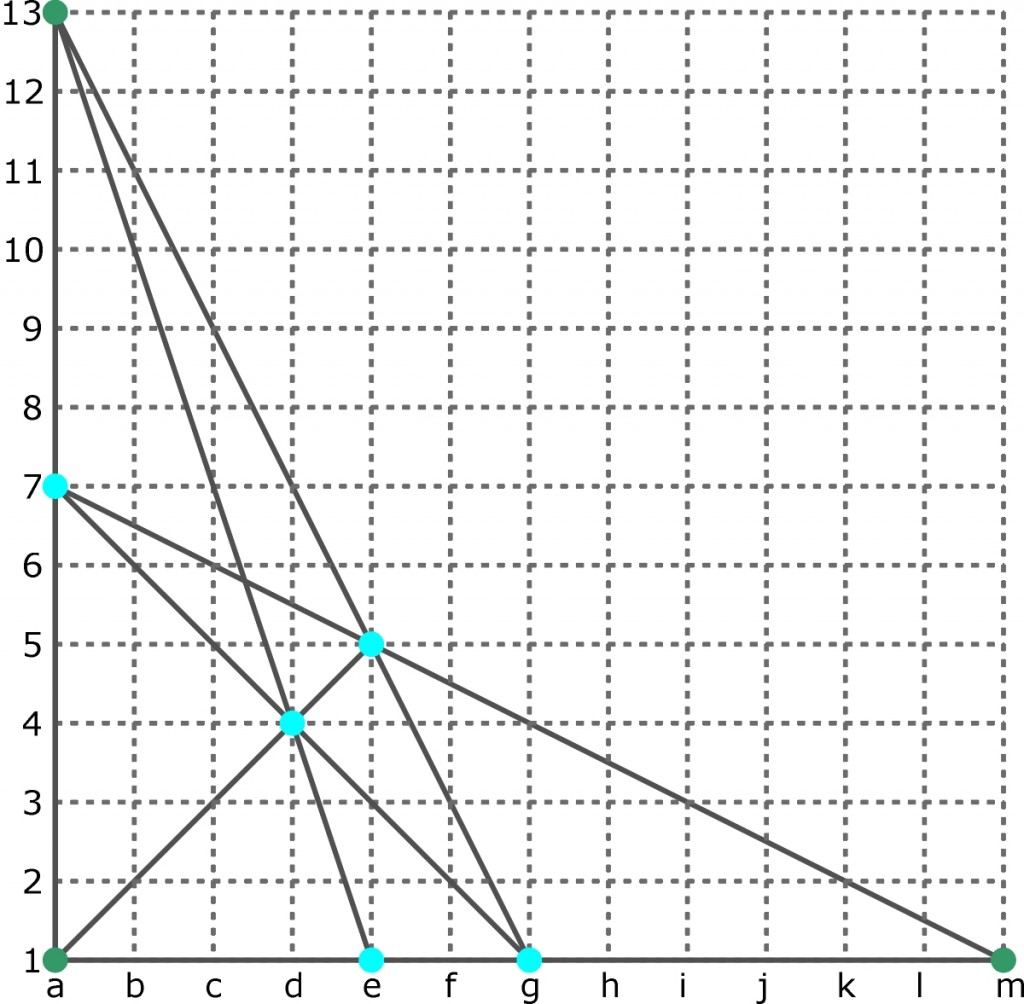
Na zmaganie się z tym zadaniem, podobnie jak na cały problem sadzenia drzew, nie ma uniwersalnej metody. Trzeba próbować i kombinować, co też czyniłem i znalazłem następujące rozwiązanie: pięć drzew tkwi w punktach a7, d4, e1, e5, g1. Graficznie, z zaznaczonymi siedmioma rzędami, wygląda to tak:
Co ciekawe, konsultant też wpadł na takie rozwiązanie, a na żadne inne nie, co utwierdziło mnie w podejrzeniu, że innego nie ma. Jakież więc było moje zdziwienie, gdy okazało się, że żadna z blisko setki osób, uczestniczących w konkursie, nie nadesłała takiego rozwiązania.
Ile różnych rozwiązań ma to zadanie – nie wiem, a ile różnych nadesłali czytelnicy – na razie nie ujawnię. Być może niektórzy z Państwa spróbują znaleźć i nadesłać choć jedno – oczywiście inne niż podane wyżej – i może będzie wśród nich takie, którego nie znam. Wszystkie staro- i nowoodkryte podam za kilka dni, o ile ktoś z Państwa wcześniej do cna nie rozgryzie tego zadania.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
Oczywiście od razu rzuca się w oczy rozwiązanie będące lustrzanym odbiciem do podanego wyżej (a7, d4, e1, e5, g1), czyli:
a5 a7 g1 d4 e5.
Osią symetrii jest prosta przechodząca przez punkty d4, e5.
Czyli tak naprawdę, tylko e1 przechodzi na a5. Mała zmiana, ale jednak zmiana.
Całkiem zgrabne jest też:
a7 d4 e5 g1 g7. Ale takie kombinowanie mniej mnie cieszy (chyba, że zdaję sobie sprawę z faktu, że kombinowanie doprowadzi mnie do jednoznacznego rozwiązania).
Mógłbym poszukać inspiracji w podręcznikach do krystalografii, ale rozwiązania wymyślone zawsze cieszy bardziej od znalezionego.
To dziwne, że zarówno Pan jak i konsultant nie wpadli na inne rozwiązanie. Bo wg mnie od razu rzuca się w oczy, że przesunięcie drzewa z e1 na g7 tworzy poprawne rozwiązanie – I na dodatek bardzo symetryczne.
Szukam dalszych.
Piotr
Dobrze jest sobie trochę poobracać proste w głowie, a pojawiają się nowe rozwiązania, np.:a11, g4, h1, h5, j1. Ciekawe czy gdybym najpierw natrafił na zadanie w Świecie Nauki czy też bym wpadał na różne możliwe kombinacje. Od wielu lat, od tej właśnie rubryki rozpoczynam lekturę tego czasopisma, ale akurat tego zadania jeszcze nie rozwiązywałem.
Strzelam w ciemno, że równie dobrym rozwiązaniem będzie a9, a10, d7, e9, j1 (odbicie rozwiązania powyższego).
Podsumujmy:
1) a5 a7 d4 e5 g1
2) a7 d4 e5 g1 g7
3) a11, g4, h1, h5, j1
4) a9, a10, d7, e9, j1
Sądzę, że warto się zastanowić nad ogólnymi warunkami, które muszą spełniać możliwe, poprawne rozwiązania.
W podanych przeze mnie, przez każdy punkt stojący na prostych które przecinają co najwyżej 3 punkty, przechodzą 3 proste. Natomiast w przypadku punktów stojących w rzędzie składającym się z 4 punktów, 2 punkty są przecinane przez 3 proste oraz 2 przez 2 proste. Trochę to zawiłe, ale prawdziwe.
Daje to pewną wskazówkę, gdzie należy postawić kolejny punkt, gdy np.: nie chcemy stawiać nawet jednego punktu na prostych a1-m1 oraz a1-a13.
Ale na dzisiaj dość już tych przemyśleń, zbliża się weekend, więc może mi się uda, jak to ujął pan Marek, rozgryźć łamigłówkę do cna. Będę próbował.
Inne rozwiązanie zadania, to np.
– a7, d4 ( albo d7, albo g4 ), e5, g1, g7.
Ciekawe są ścieżki, którymi kroczą umysły Gospodarza i jego konsultanta. Znaleźć przykład (chyba trudniejszy do wypatrzenia) rozwiązania zadania, którego blisko setka główkołamaczy nie znalazła, a nie wpaść na trop rozwiązań którymi konkursowicze się pochwalili.
To daje do myślenia.
Jak rozumieć – „nie ma uniwersalnej metody rozwiązywania problemu sadzenia drzew w rzędach” – ?
– (1) Nie ma, dlatego, że istnieje dowód na brak takiej metody.
– (2) Nie ma, bo nikt do tej pory nie znalazł takiej metody.
(2) oczywiście. Jakoś nie przychodzi mi do głowy jakikolwiek konkretny dowód na nieistnienie jakiejś metody.
mp
Tak na szybkiego, dwa, symetryczne rozwiazania:
a(1,5,13),c3,d4,e1,g7,m1
i ładniejsze:
a(1,7,13),d4,e5,g(1,7),m1
1) a7,g1,d4,e5,g7
2) a5,e1,c3,d4,g7
Dopiero teraz zauważyłem, że to moje drugie rozwiązanie różni się od autorskiego innym rozmieszczeniem tylko jednego punktu, to znaczy drzewa:)