Multikropka
Pokropka ma dość dobre notowania. Główkołamacze uznali ją swego czasu za najciekawszy rodzaj zadania made in Japan spośród tych, które gościły w dodatku do Polityki przed ponad dwoma laty (Wakacje z głową); w pobitym polu znalazło się nawet sudoku. Mimo to nigdzie poza Japonią, nawet w wyczulonej na ciekawe pomysły prasie brytyjskiej, nie była lansowana jako kandydatka na przebój. A to dlatego, że zdaniem speców od robienia w tej dziedzinie „zamieszania”, jeśli w łamigłówce nie wpisuje się czegoś w kratki, jak w krzyżówce i sudoku, to nie warto zawracać nią sobie głowy.
Pomysł był jednak przed laty bardzo oryginalny i prosty, a zabawa okazała się wciągająca. Przypominam krótko zasady.
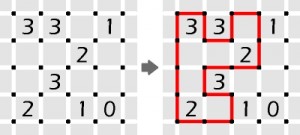
W siatkę kwadratową należy wrysować linię łamaną zamkniętą pokrywającą się z liniami siatki i nie goszczącą dwukrotnie w tym samym punkcie; cyfra w kratce oznacza, ile boków tej kratki powinno być fragmentami łamanej.
I przykład:
W diagramach linie siatki są z reguły pomijane, pozostają tylko skrzyżowania, czyli kropki.
Pokropce stuknie niedługo 20 lat. Różnych nazw ma mniej więcej tyle samo. Przyszła na świat w japońskim wydawnictwie Nikoli jako suriza rinku, czyli „pełzające (ślizgające się) ogniwo (pierścień)”. Tę nazwę oraz jej angielski odpowiednik – slitherlink, wydawca umieścił w metryce i zastrzegł, więc nic dziwnego, że pojawiło się wiele „pseudonimów”. W Polsce zaproponowałem 9 lat temu określenie „pokropka”, które chyba się przyjęło. Ostatnio zwolennicy czarnego humoru proponują zmianę rodzaju na męski – „pokropek”, czyli wg SJP: „pokropienie zwłok wodą święconą przed złożeniem ich do grobu”.
Pokropka jest dobrym sposobem na zabicie czasu i rozruszanie szarych komórek. Łatwo wciąga, ale też łatwiej niż reszta szablonowej japońszczyzny zaczyna przynudzać. Głównie dlatego, że z jednej strony sporo w niej schematyzmu związanego z układami cyfr, od których zaczyna się rozwiązywanie (ładnie opisane w Wikipedii) oraz z układami linii, pojawiającymi się w trakcie rozwiązywania, zaś z drugiej strony nierzadko trafiają się, zwłaszcza w większych zadaniach, fragmenty bliższe drodze przez mękę, niż rozrywce. Kiedy więc wchodzę do odpowiedniego działu hurtowni łamigłówek państwa Janko i widzę grubo ponad pół tysiąca pokropek, to czuję się trochę dziwnie i czym prędzej wracam do normalności.
Choć łamigłówka nie była lansowana na szerszym forum, to w Internecie łatwo na nią trafić. Gdybym miał polecić jakąś stronę do zabawy, byłoby to chyba japońskie Puzzle museum, bo jest ładne graficznie i oferuje niewiele zadań, ale za to starannie opracowanych i lekkostrawnych. A gdybym miał zaproponować coś ciekawego ambitnym łamigłówkowiczom, to byłoby to nieduże, ale dość trudne zadanie, z ograniczoną możliwością stosowania prostych schematów, na przykład taka 121-kropka:
Na wszelki wypadek uzupełniłem diagram literami, bo może ktoś zechce się pochwalić rozwiązaniem, podając współrzędne kratek otoczonych łamaną. Wersja odpowiedzi dla leniwych: których kratek jest więcej w rozwiązaniu i o ile więcej – otoczonych łamaną, czy pozostających poza nią?


Komentarze
Kratki wewnątrz pętli:
A abdhi
B abdhij
C abcdefghi
D cdi
E di
F acdegij
G abcghi
H abcfghi
I cg
J cgh
Aabdhi, Babdhij, Cabcdefghi, Dcdi, Edi, Facdegij, Gabcghi, Habcfghi, Icg, Jcgh
to odpowiedź na pierwsze zadanie.
odpowiedź na drugie pytanie to: kratek jest po tyle samo „w” jak i „poza” pętlą
pzodrawiam
Kratek otoczonych łamaną jest tyle samo co poza nią.
Aa,Ab,Ad,Ah,Ai
Ba,Bb,Bd,Bh,Bi,Bj
Ca,Cb,Cc,Cd,Ce,Cf,Cg,Ch,Ci,
Dc,Dd,Di,
Ed,Ei,
Fa,Fc,Fd,Fe,Fg,Fi,Fj,
Ga,Gb,Gc,Gg,Gh,Gi,
Ha,Hb,Hc,Hf,Hg,Hh,Hi,
Ic,Ig,
Jc,Jg,Jh.
Jestem leniwa: kratek „in” jest tyle samo co „out”.
Poza tym lubię czarny humor, ale bez przesady, więc wolę rodzaj żeński.
Zz
Warunek konieczny, ale nie wystarczający:
51(w)-49(z)=2.
Warunek wystarczający:
Aa, Ab, Ad, Ah, Ai,
Ba, Bb, Bd, Bg, Bh, Bi, Bj,
Ca, Cb, Cc, Cd, Ce, Cf, Cg, Ch, Ci,
Dc, Dd, Di,
Ed, Ei,
Fa, Fc, Fd, Fe, Fg, Fi, Fj,
Ga, Gb, Gc, Gg, Gh, Gi,
Ha, Hb, Hc, Hf, Hg, Hh, Hi,
Ic, Ig,
Jc, Jg, Jh.
Pozdrawiam
Kratki otoczone łamaną:
A:a,b,d,h,i
B:a,b,d,h,i,j
C:a,b,c,d,e,f,g,h,i
D:c,d,i
E:d,i
F:a,c,d,e,g,i,j
G:a,b,c,g,h,i
H:a,b,c,f,g,h,i
I:c,g
J:c,g,h
Znając dowcip Pana Marka 😉 można by w ciemno podać rozwiązanie zagadki – kratek będzie tyle samo wewnątrz i na zewnątrz. Jednak cała przyjemność to sprawdzenie tego samemu.
Z pokropką zetnąłem się bardzo niedawno i jeszcze nie jest dla mnie nudząca, lecz bardzo męcząca, a przedstawione zadanie jest chyba szczególnie „wredne” – nie chodzi o brak schematów (bo te przydać się mogą chyba tylko rozwiązując zadanie na czas), ale o głębokość z jaką trzeba analizować eliminowanie kresek. To tak, jakby wejść do jaskini i po przejściu kilku kilometrów wracać, żeby wybrać inny korytarz.
Widzę, że znowu nie udało mi się poprawnie rozwiązać zadania. Może następnym razem lepiej mi pójdzie.
Wydawnictwo Logi serwuje łamigłówkę jako „wielokropki”. Na http://www.obrazkilogiczne.pl/wielokropki.php można znaleźć kilka diagramów, instrukcję oraz wskazówki rozwiązywania.
Pozdrawiam 😉
Niezłe jeszcze nie rozwiązałam ale próbuje to świetna zabawa!!!