Szczypta złota
Dziesiątki, a może i setki werdyktów Łamiblogowej „ławy przysięgłych” zawarte w komentarzach, które nie pojawiły się po poprzednim wpisie, świadczą o tym, że decyzję rozstrzygającą o winie lub niewinności korporacji Kimberly-Clark podjąć jest bardzo trudno albo podejmować jej nie warto. Decyzja o takim potraktowaniu tej decyzji jest prawidłowa i nikt przedtem nie zdecydował się na jej podjęcie, nawet sąd brytyjski. Moja informacja, że tak było, to mistyfikacja. Przepraszam tych, którzy szukali potwierdzenia tego faktu w Internecie. Można wprawdzie trafić na parę informacji sugerujących wygraną profesora Penrose’a i duże odszkodowania, ale są to tylko domniemania lub pobożne życzenia.
Roger Penrose nadał przed laty spory rozgłos sprawie wykorzystania jego mozaik jako wzoru na papierze toaletowym i zapowiedział proces, jednak w porę się zreflektował. Po pierwsze dlatego, że zastrzeżenie odkrycia naukowego było przynajmniej dyskusyjne, mimo że chodziło o wzór geometryczny (na podobnej zasadzie można by zastrzec wstęgę Moebiusa). Istotniejsze jednak, że sir Penrose dowiedział się poniewczasie, iż w związku z upływem lat ważność jego patentu wygasła, zatem roszczenia na drodze prawnej nie miały podstaw.
Początkowo firma Kimberly-Clark potraktowała zarzuty uczonego z przymrużeniem oka, między innymi rozpowszechniając informację, jakoby odkrywca mozaik domagał się zniszczenia gigantycznej partii wyprodukowanego papieru toaletowego. Roger Penrose był już jednak wówczas osobą znaną, luminarzem nauki i VIP-em z tytułem szlacheckim, toteż niebawem dzięki pośrednictwu doszło do przeprosin i rozmów zakończonych ugodą. Jej szczegółów nie upubliczniono.
Wspominałem poprzednio o zagadkowym związku między 2-elementowymi, aperiodycznymi mozaikami Penrose’a, a złotym podziałem. Zagadka jest szczególna, bo złoty podział to zjawisko matematyczne niemal z pogranicza mistyki, choć można je określić trywialnie: podział całości na dwie nierówne części jest złoty, gdy całość ma się tak do większej części, jak większa część do mniejszej. Stosunek ten wyraża się złotą liczbą, oznaczaną grecką literą fi, równą (1 + sqrt5)/2, czyli 1,61803398…
W przypadku każdej 2-elemetowej mozaiki Penrose’a nie tylko stosunek długości określonych odcinków tworzących figury składowe wyraża się złotą liczbą, ale jest nią także stosunek liczby jednego rodzaju figur do drugiego w nieskończonej mozaice. Dlaczego tak jest, to dotąd nierozwiązana zagadka. Natomiast poniższa łamigłówka jest znacznie prostsza i być może zachęci Państwa do przypomnienia sobie podstawowych wiadomości na temat złotego podziału oraz do poczytania, choćby w Wikipedii, o ciekawostkach związanych z tym szlachetnym rąbkiem matematyki.
Proszę rozwiązać poniższe równanie, czyli znaleźć wartość x. Na wszelki wypadek, gdyby ktoś po rzuceniu okiem postanowił natychmiast zmienić kanał, przypominam, że to nie zadanie rachunkowe z akademickiego podręcznika tylko łamigłówka matematyczna, w dodatku nieco żartobliwa; grecka litera w równaniu to właśnie fi, czyli złota liczba.
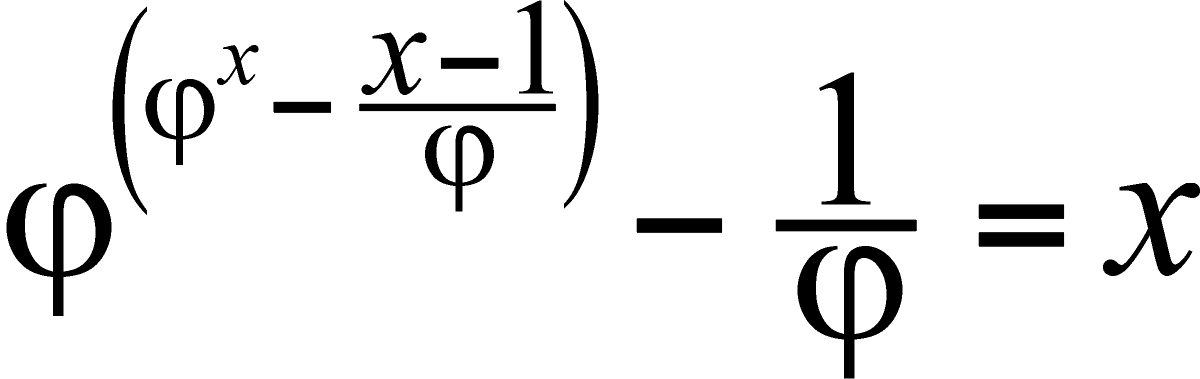
PS nadsyłane rozwiązania uwolnię za kilka dni, tuż przed następnym wpisem.

Komentarze
Odpowiedz to x=2.
Chetnie zobacze jakies ciekawe rozwiazanie, bo przyznaje niestety, ze ja rozwiazywalem metoda „na sile”, czyli wstawilem pod x kolejno fi,fi^2,0,1,2 …
x=2
Z własności „złotej liczby” : ??-1/?=2 łatwo obliczyć, że x=2.
Pozdrawiam.
Jr
Poprawiłem zapis:
Z własności „złotej liczby” : sqrt(fi)-1/fi=2 łatwo obliczyć, że x=2.
Pozdrawiam.
Jr
Rozwiązaniem jest x=2
x=2
Może istnieją jeszcze inne rozwiązania.
Jak do tego doszedłem? Ano przy pomocy znanego „wytrycha”:
1. Przyjąłem początkową wartość x=0.
2. Podstawiłem pod x po lewej stronie równania.
3. Wyliczyłem wartość x (prawa strona równania).
4. Znów podstawiłem nową watrtość pod x po lewej stronie otrzymując następną wartość x.
5. Itd po kilku krokach widać, że x prawdopodobnie dąży do 2.
Później tylko sprawdziłem, czy x=2 rzeczywiście spełnia równanie.
Wiem, że metoda – jak na łamigłówkę – jest niezbyt elegancka, ale czasem skuteczna.
Przy okazji warto zauważyć, że
fi – 1 = 1/fi
czyli część ułamkowa fi jest równa odwrotności fi.
Może to pomóc w znalezieniu ciekawszej metody.
Odp: X=2
Moja idea dojścia do rozwiązania była następująca:
1) Zauważyłem, że (1+1/fi)=fi,
2) Przeniosłem (-1/fi) na prawą stronę równania,
3) Podstawiłem x = z + 1, a zatem po prawej stronie równania miałem: z + fi; dokonałem też przekształceń po lewej stronie równania, na skutek podstawienia za x wyrażenia z+1 (podstawienie w ogóle nie było konieczne, ale ułatwiło mi „zauważenie” drogi do rozwiązania i okazało się dla mnie „strawniejsze” niż początkowa postać równania),
4) Założyłem sobie na początek dla uproszczenia, że liczba z jest całkowita (tak po prostu przypuszczałem – informacja od Autora, że zadanie nie jest takie trudne na jakie wygląda też jest jakąś wskazówką). Problem sprowadził się do poszukiwania takiej liczby, że fi podniesione do tej potęgi da jakąś liczbę zakończoną „ogonkiem” (czyli 0,618033…),
5) Po podniesieniu fi do kwadratu od razu okazało się, że wynik ma „ogonek”, bo jest nim 2,618033…,
6) Wynikało z tego, że z=1, bo 1+1,618033…=2,618033…,
7) Pozostało sprawdzić czy wyrażenie w potędze po lewej stronie równania wynosi 2 dla z=1. Okazało się, że tak jest.
8) Skoro x=z+1, to x=2 i mamy rozwiązanie.
Być może nie jest to jedyne rozwiązanie, ale podejrzewam, że właśnie o taką odpowiedź chodziło w zadaniu.
Gospodarz blogu – Pan Marek Penszko napisał:
„W przypadku każdej 2-elemetowej mozaiki Penrose’a nie tylko stosunek długości określonych odcinków tworzących figury składowe wyraża się złotą liczbą, ale jest nią także stosunek liczby jednego rodzaju figur do drugiego w nieskończonej mozaice.”
I tu mam wątpliwości. Albo nie znam jakiegoś założenia, które należy spełnić przy układaniu mozaiki albo powyższy cytat nie głosi prawdy.
Przecież możliwe jest ułożenie nieskończonej mozaiki zawierającej elementy tylko jednego rodzaju. Mało tego, możliwe jest również ułożenie mozaiki zawierającej nieskończenie wiele elementów jednego rodzaju i dowolną skończoną albo nieskończoną liczbę elementów drugiego rodzaju. O przykłady nie trudno.
Zatem jak to jest z tymi mozaikami?
Jaz_onie, taką mozaikę 1- lub 2-elementową, jaką opisałeś, można oczywiście ułożyć, ale nie będzie to mozaika Penrose’a, której cechą charakterystyczną jest m.in. to, że układana jest zgodnie z określonymi zasadami. Zasady te, w przypadku mozaiki z rombów, są ładnie przedstawione na rysunku w angielskiej Wikipedii (http://en.wikipedia.org/wiki/Penrose_tiles) – rozdział „Rhombus tiling (P3)”.
Pozdrawiam
mp
Czyli istnieje jeden warunek mówiący, że żadne dwa stykające się elementy nie mogą tworzyć równoległoboku. To rzeczywiście znacznie ogranicza możliwości budowania parkietaży, dając jednocześnie tak ciekawe ich właściwości.
Niezależnie od tego, interesujące jest, czy zastanawiał się ktoś nad wersją trójwymiarową tego zagadnienia, tj. nad nietrywialnym wypełnianiem przestrzeni odpowiednio dobranym zestawem prostych brył z prostymi zasadami ich łączenia.
Z pozdrowieniami,
Jaz_off
Przestrzennym odpowiednikiem rombowej mozaiki Penrose’a są sieci Ammana-MacKaya, występujące np. w kwazikryształach. Romby sa w nich zastąpione równoległościanami. Niestety, w Internecie jest na ten temat bardzo niewiele, a w formie popularnej nie ma chyba nic.
Przykładem przestrzennej mozaiki aperiodycznej do obejrzenia jest quaquaversal Conwaya http://www.ma.utexas.edu/users/radin/quaqua.html będący odpowiednikiem płaskiego „wiatraczka” http://www.ma.utexas.edu/users/radin/pinwheel.html
mp
no no ciekawe nawet na tak daramatyczne me serce ale ja ni mugl bym tak to zrobic bo jestem slepcem takie me zycie prosze niespulczuc i to nie ja pisalem tylko ma asystentke 🙂
x=2 Banał ;D