Kwadratowo
Rok „potężny” za pasem, choć to tylko druga potęga z podstawą równą 45. Poprzedni kwadratowy był 89 lat temu (1936), a następny będzie za lat 91 (2116).
Liczbowe panoptikum można zacząć właśnie od przełomu 2024/2025. Takie pary kolejnych liczb (całkowitych dodatnich) to rzadkość. Mniejsze znane są tylko dwie – 35/36 i 120/121, a większe tylko trzy. Poszukiwaniu siódmej pary komputery na razie nie podołały i jest bardzo prawdopodobne, że nie istnieje. Odpowiedź na pytanie, na czym polega ta parzysta osobliwość, niełatwo odkryć, ale można znaleźć, jeśli się wie, gdzie jej szukać.
W przypadku 2025 jako kwadratu warte uwagi kurioza są przynajmniej dwa. Pierwsze proste: 2025 pozostaje kwadratem, jeśli każdą cyfrę zwiększyć o 1 (3136=56^2). Sąsiednie kwadraty o tej własności to 25 i 13225. Większe szybko stają się gigantami.
Drugie kuriozum ma postać 2025=(20+25)^2. Tu analogicznych przypadków (składanie podstawy kwadratu z jego połówek) są krocie, ale trudno na nie trafić, bo tkwią wśród liczb naturalnych jak rodzynki w cieście, np. przed 10000 są oprócz 2025 ledwie trzy – 81, 3025 i 9801.
Można jeszcze odnotować fakt, że kwadrat 2025 jest sumą dwóch kwadratów, przy czym jest tylko jedna taka para. Jaka?
A na koniec proste klasyczne „przełomowe” zadanie typu „3 po 3”.
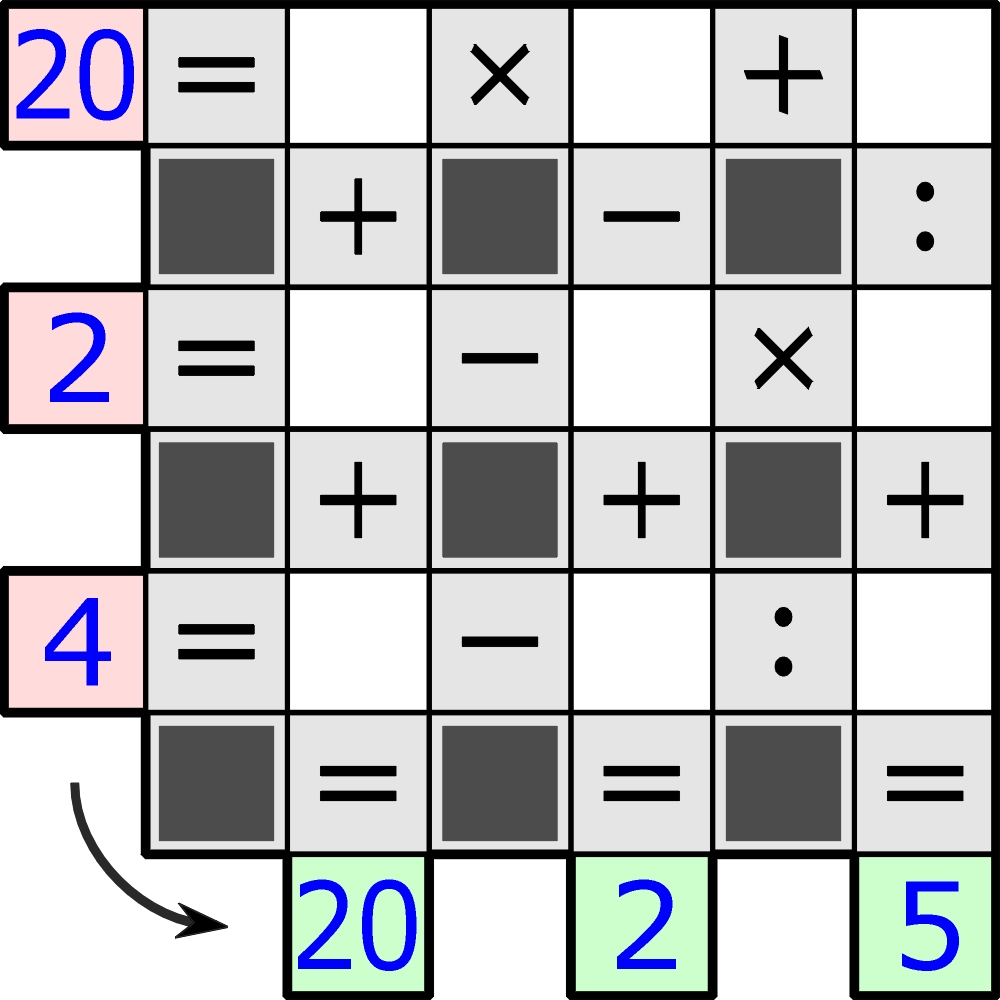
Chodzi oczywiście o rozmieszczenie w kratkach cyfr od 1 do 9 tak, aby działania w trzech wierszach i trzech kolumnach były poprawne. Działania w każdym rzędzie należy wykonywać po kolei, czyli bez uwzględniania pierwszeństwa mnożenia i dzielenia (uwaga ta dotyczy właściwie tylko drugiego i trzeciego wiersza).
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
2024 jest liczbą czworościenną postaci kwadrat pewnej liczby -1
2025=36×36+27×27
438
762
951
Szczęśliwego Nowego Roku dla wszystkich łamigłówkowiczów!
Konkatenuję się.
mp
20=4×3+8
2=7-6×2
4=9-5:1
4+7+9=20
3-6+5=2
8:2+1=5
Pozdrawiam
A.
3 po 3:
4, 3, 8,
7, 6, 2,
9, 5, 1
27^2 + 36^2 = 2025 = 729 + 1296
Dołączam do życzeń noworocznych:)
A rozwiązanie to:
4 3 8
7 6 2
9 5 1
2025 = 27^2 + 36^2
Z życzeniami wszystkiego dobrego w Nowym Roku dla prowadzącego tę wspaniałą rubrykę i dla wszystkich rozwiązujących. A dla miłośników kryptarytmów zadanie, które kiedyś zdarzyło mi się ułożyć. Ma tylko jedno rozwiązanie: TO * ROKU ------- ??? ?? ??? ??? ======= KONIEC Dla ułatwienia rozwiązania: - sumy cyfr mnożnej, mnożnika i iloczynu to (kolejno) - 11, 18 i 27, - brakująca cyfra nie pojawia się również w żadnym iloczynie cząstkowym.27^2 + 36^2=2025
Zadanie przełomowe
4,3,8
7,6,2
9,5,1
Kryptarytm
38*4815=182970
2025 = 1 ^3 + 2^ 3 +3^3+4^3+5^3+6^3+7^3+8^3 + 9^ 3
2025 = T44 + T45 (44 i 45 liczba trójkątna 990 i 1035)
Zadanie 3 po 3:
438
762
951
Suma kwadratów:
45 dzieli się przez 5, więc możemy otrzymać trójkąt egipski, czy też pitagorejski w skali 9:1 – 27, 36, 45; 729+1296 = 2025.
Zagadka grgkh:
38
4815
182970
Oprócz opisanej, ciakwej właściowości liczby 2025 czyli kwadratu liczby 45 a więc kwadratu sumy wszystkich cyfr (od 1 do 9) jest jeszce inna, ciekawsza mianowicie 2025 to suma sześcianów wszystkich cyfr.
W nowym roku moc uścisków!
dużo zdrowia i pomysłów.
Masyu gościło na łamach Łamibloga we wrześniu 2021
https://penszko.blog.polityka.pl/2021/09/11/reka-diabla/
https://penszko.blog.polityka.pl/2021/09/18/masyu-prequel/
Przepisane reguły z „Ręki diabła” dla masyu brzmią tak:
Białe i czarne koraliki umieszczone w niektórych kratkach diagramu należy nawlec na nitkę,
czyli połączyć jedną linią łamaną zamkniętą złożoną z odcinków równoległych do brzegów diagramu,
przechodzących przez środki kratek. Łamana musi się załamywać w każdym czarnym koraliku oraz w polu
tuż przed lub/i tuż za białym koralikiem. Łamana nie może się załamywać w żadnym białym koraliku,
ani w polach tuż przed i tuż za czarnym koralikiem.
Ponieważ jest już rok 2025, do ewentualnego wykorzystania
░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│
░│░│B│B│░│░│░│B│B│░│░│░│B│B│░│░│C│B│B│C│░│
░│B│░│░│B│░│B│░│░│B│░│B│░│░│B│░│B│░│░│░│░│
░│░│░│░│C│░│B│░│░│B│░│░│░│░│B│░│B│B│B│░│░│
░│░│B│B│░│░│B│░│░│B│░│░│B│B│░│░│░│░│░│B│░│
░│B│░│░│░│░│B│░│░│B│░│C│░│░│░│░│B│░│░│B│░│
░│B│B│B│B│░│░│B│B│░│░│B│B│B│B│░│░│B│B│░│░│
░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│░│
Diagram 21×8
B-białe kółko C-czarne kółko ░-puste pole
Rozwiązanie
░ ░ ┌ ┐ ░ ░ ░ ┌ ┐ ░ ░ ░ ░ ░ ░ ┌ ─ ─ ─ ─ ┐
░ ░ │ │ ░ ░ ░ │ │ ░ ░ ┌ ─ ─ ┐ │ ┌ ─ ─ ┐ │
┌ ─ ┘ └ ─ ─ ─ ┘ └ ─ ┐ │ ░ ░ │ │ │ ┌ ┐ │ │
│ ░ ┌ ┐ ┌ ─ ─ ┐ ┌ ─ ┘ │ ┌ ┐ │ │ │ │ │ └ ┘
└ ┐ │ │ │ ┌ ─ ┘ └ ─ ─ ┘ │ │ └ ┘ └ ┘ └ ─ ┐
░ │ │ │ │ └ ─ ┐ ┌ ─ ─ ┐ │ │ ┌ ─ ─ ┐ ┌ ─ ┘
░ │ │ │ │ ░ ░ │ │ ░ ░ │ │ │ │ ░ ░ │ │ ░ ░
░ └ ┘ └ ┘ ░ ░ └ ┘ ░ ░ └ ┘ └ ┘ ░ ░ └ ┘ ░ ░
Dziękuję. Z przyjenością wykorzystam w Łamiblogu.
Pozdrawiam noworocznie
mp
@grgkh
38 * 4815 = 182970
oba warunki ułatwiające nie są potrzebne.
nie są potrzebne również formaty iloczynów cząstkowych.
mowa oczywiście o podejściu siłowym 🙂
Przełomowego Nowego Roku dla Wszystkich Łamiblogowiczów
20=4*3+8
2=7-6*2
4=9-5:1
pionowo:
4+7+9=20
3-6+5=2
8:2+1=5
pozdrawiam
w istocie jest tylko jedna para z przedostatniego akapitu: kwadraty liczb 27 i 36 tworzą w sumie 2025
Zagadki związanej z parami kolejnych liczb naturalnych nie odgadłem, ale wiedziałem, gdzie można szukać odpowiedzi. Prawdopodobnie chodzi o liczby czworościenne postaci k^2 – 1.
@grgkh
TO: liczba 19-gładka,
ROKU i KONIEC: liczby 107-gładkie.
1296+729
4, 3, 8
7, 6, 2
9, 5, 1
@jacekstu
Okazuje się, że to, iż kwadrat sumy i suma sześcianów kolejnych liczb są sobie równe, jest prawdziwe dla wszystkich n, nie tylko 9. Dla n = 1 jest to oczywiste, dla n = 2 mamy (1+2)^2 = 1^3+2^3 = 9, dla n = 3 jest (1+2+3)^2 = 1^3+2^3+3^3 = 36, itd. Dowód jest indukcyjny: z faktu, że (1+…+(n-1))^2 = 1^3+…+(n-1)^3 wynika, że (1+…+n)^2 = 1^3+…+n^3.
Jeśli przez S(n) oznaczymy sumę kolejnych liczb od 1 do n, to po lewej stronie mamy (S(n-1)+n)^2 = (S(n-1))^2+2*n*S(n-1)+n^2. Z założenia indukcyjnego pierwszy składnik jest równy sumie sześcianów od 1 do n-1, potrzeba więc udowodnić, że suma dwóch pozostałych składników jest równa n^3. Mamy:
2*n*S(n-1)+n^2 = 2*n*(n-1)*n/2 + n^2 = 2*n^3/2 – 2*n^2/2 +n^2 = n^3 – n^2 + n^2 = n^3, cnd. Skorzystaliśmy ze znanego wzoru: S(n-1) = (n-1)*n/2.
Potrzeba było, żeby przyszedł rok 2025, żebym sobie to uświadomił i udowodnił…