O drugim byczku
Dziś miało być bez byczka, ale w międzyczasie uważni i życzliwi Czytelnicy poinformowali mnie o innym „Omnibusowym” okazie, który uszedł mojej uwadze. To byczek podobnego rodzaju, jak pierwszy, bo ukryty w instrukcji, ale nieco większego kalibru. Ponieważ jego szukanie może stanowić umysłową zabawę w chowanego, więc postanowiłem o nim napomknąć.
Chodzi o zadanie Koraliki (s. 14). Cytuję „rogatą” instrukcję:
Wszystkie kolorowe kółka należy jak koraliki nawlec na nitkę, czyli połączyć linią łamaną zamkniętą, biegnącą białymi drogami. Linia ta nie może przecinać samej siebie, a ponadto:
a) powinna załamywać się:
– w każdym zielonym kółku
– w kratce tuż przed lub/i tuż za „zaliczonym” pomarańczowym kółkiem
b) nie może załamywać się:
– w żadnym pomarańczowym kółku,
– w kratce tuż przed lub/i tuż za „zaliczonym” zielonym kółkiem.
I przykład:
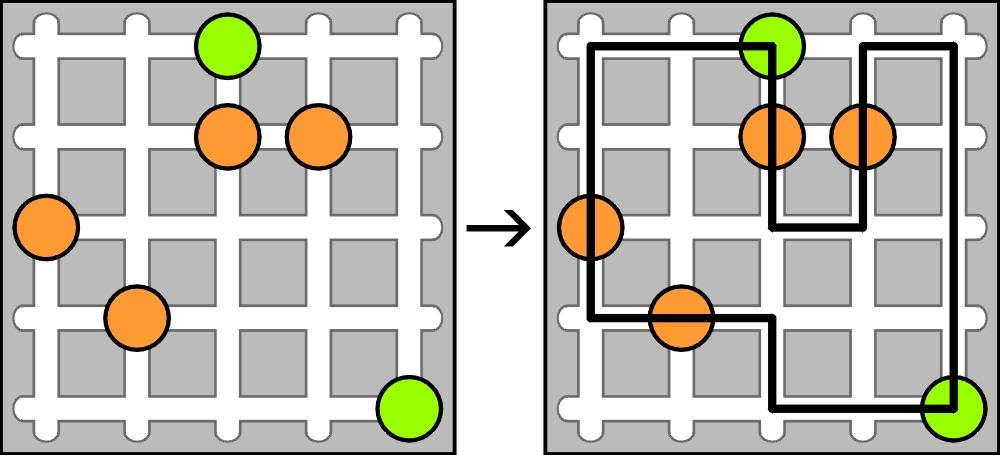
A pytania są dwa:
1) gdzie jest błąd w instrukcji, jeśli uznać, że rozwiązanie przykładu jest jedynym możliwym;
2) jeśli przyjąć, że błędu nie ma, to ile rozwiązań ma zadanie przykładowe.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
O, faktycznie jest błąd w instrukcji. Rozwiązując to zadanie nawet nie zwróciłem na to uwagi, bo dobrze znam reguły łamigłówki Masyu i po pobieżnym przeczytaniu byłem pewien że to dokładnie ta sama
Chodzi zapewne o „i/lub” w punkcie b), co sugerowałoby, że przynajmniej w jednym polu przed i po zielonym koraliku linia musi iść prosto, podczas gdy w oryginalnym Masyu musi iść prosto w obu tych przypadkach (czyli w instrukcji powinno być „i”).
W linku jedno z rozwiązań, których ilość jest silnie uzależniona od rozdzielczości obrazka.
https://zapodaj.net/plik-DIbr3eAWVM
Taką mam koncepcję
Wyszło mi aż 10 rozwiązań przykładu, zakładając brak błędu w instrukcji.
W zasadzie ułożenie zielonych koralików w tym przypadku wymusza to, że w co najmniej jednym polu obok (wzdłuż linii) będzie linia prosta.
Hmm nie jestem pewien czy w dobrą stronę idę, ale drugą część punktu b bym sformułował:
„Nie może załamywać się w kratce tuż przed zaliczonym zielonym kółkiem i nie może się załamywać w kratce tuż za zaliczonym zielonym kółkiem”
To „lub/i” nie wiem w jaki logiczny spójnik zamienić ale to wydaje się mieszać.
a lub/i b = (a lub b) lub (a i b)
A alternatywnych rozwiązań, gdzie drugi warunek pkt b brzmi
„Nie może załamywać się w kratce tuż przed zaliczonym zielonym kółkiem lub nie może załamywać się w kratce tuż za zaliczonym zielonym kółkiem”
Wychodzi mi 10.
1) Brakuje: „Na białej drodze mieści się tylko jedna nitka” (na skrzyżowaniu też).
2) Nieskończenie wiele
Nie jest jasne co znaczy: „w kratce tuż przed lub tuż za … „. Co jest ową kratką? Białe linie krzyżują się tworząc kratkę, na przykład taką, jaką ustawiamy w ogrodzie, aby pięły się po niej rośliny. Ale wewnątrz kratownicy białych dróg możemy wyróżnić kwadratowe segmenty, które też nazwiemy kratkami, podobnie jak ma to miejsce w Excelu. Zamiast „w” można by powiedzieć : „o kratkę przed lub o kratkę tuż za”. Domyślamy się, że załamania mogą nastąpić na skrzyżowaniach białych dróg. Instrukcja tego nie precyzuje, a skoro tak, to nitka biegnąc drogą między skrzyżowaniami może dokonać załamania o 180 stopni i wrócić biegnąc równolegle obok samej siebie do najbliższego skrzyżowania i tam pożegnać się sama ze sobą wybierając inną trasę.
Instrukcja powinna brzmieć w punkcie b tak:
b) nie może załamywać się:
– w żadnym pomarańczowym kółku,
– ani w kratce tuż przed ani w kratce tuż za „zaliczonym” zielonym kółkiem.
Bez tej poprawki jest moim zdaniem 9 rozwiązań (wynikających z dopuszczenia załamania linii tuż za lub tuż przed zielonym kółkiem, ale nie z obu stron)
Naturalnie tutaj od razu można by rozpocząć dywagacje o spójniku „lub”, czyli ulubionemu słowu prawników i logików. Ja nie widzę sensu w spójniku „lub/i” i tym bardziej nie wiem, co to znaczy „lub/i” w przypadku przeczenia. W mojej ocenie całkowicie logicznie poprawne, ale niestety mylące, jest takie stwierdzenie:
„nie może załamywać się w kratce tuż przed lub tuż za „zaliczonym” zielonym kółkiem” > to jest w istocie zakaz załamywania się linii z jakiejkolwiek strony, ale część osób zrozumie, że dopuszczamy załamanie się linii z jednej strony
Z kolei niedopuszczalne (w kontekście tego zadania):
„nie może załamywać się w kratce tuż przed i tuż za „zaliczonym” zielonym kółkiem” > to bowiem oznacza, że zakazujemy załamania jednocześnie przed i za, ale dopuszczamy już załamanie z jednej strony.
Na koniec dodam, że całe zamieszanie bierze się stąd, że potocznie słowa „lub” i „albo” są traktowane jak tożsame, natomiast lub jest alternatywą łączną (obejmującą „i”), a albo jest alternatywą rozłączną. Czyli „albo/i” = „lub”.
W moim egzemplarzu „Omnibusa” zadanie „Koraliki” jest na 8, a nie na stronie 14. Czyżby każdy egzemplarz posiadał własną, np. losową, numerację stron?
…………………………………………………………………………………………………………….
W ostatniej chwili przed drukiem zostały przeniesione. Zapomniałem o tym i korzystałem z egzemplarza korektorskiego.
mp
Pierwszy (najmniejszy) diagram zadania „Nieskładnie”(str.26) posiada wiele rozwiązań, ale jedno z nich jest wyjątkowe. Jego unikalność polega na tym, że nie tylko dwie sąsiednie działki nie tworzą większego prostokąta, ale i więcej (oczywiście oprócz całego diagramu) działek nie będzie prostokątem.
Panie Andrzeju, wiele rozwiązań? Ile? Bo moim zdaniem 3, w tym to wyjątkowe, o którym Pan pisze. Z diagramu „uciekła” jedna zielona kreseczka.
mp
Znalazłem 4 rozwiązania:
– odpowiedź z Omnibusa
ABBBB
ACACC
ACABA
BBABA
BBCCA
-rozwiązanie wyjątkowe (najbardziej urokliwe)
ABBBB
ACCAA
ACCBC
ABAAC
CCAAC
-dwa pozostałe (niestety, do oznaczenia poniższych odpowiedzi trzy znaki nie wystarczą)
ABBBB
ACCAA
ACCBC
ABABC
ABDDC
i
ABBBB
ACAAA
ACDCC
BBDAB
BBCCB
Jeśli odpowiedź ma być taka jak w Omnibusie, to nie widzę, aby po dodaniu jednej zielonej kreseczki można było otrzymać jedno rozwiązanie.
Okazało się, że unikalność jednego z diagramów straciła swoją moc z chwilą, gdy @apartado znalazł inne urocze rozwiązanie.
Wygląda na to, że podanie wszystkich rozwiązań nie jest banalną sprawą.