Produkcyjniak
Swego rodzaju fundamentem bardzo wielu łamigłówek logicznych jest kwadratowy diagram n×n złożony z n^2 kratek. Wyobraźmy sobie profesjonalnego twórcę łamigłówek logicznych (jest paru w Japonii), który siedzi nad takim diagramem, próbując wymyślić jakiś nowy rodzaj zadania i ułożyć konkretny przykład. Mógłby zacząć od podzielenia diagramu wzdłuż boków kratek na wielokątne działki, a potem przyjąć pierwszą ogólną regułę: do jednego i tylko jednego pola w każdej działce należy wpisać liczbę równą liczbie pól tej działki.
Być może taki był początek narodzin poniższej łamigłówki. Co było dalej, czyli jakie reguły pojawiły się na następnych etapach „produkcji” – oto zagadka indukcyjna. Proponuję zatem samodzielnie ustalić te dalsze reguły na podstawie poniższego przykładu 5×5, a następnie rozwiązać zadanie 6×6. Obawiam się, że propozycja rozszyfrowania procesu produkcyjnego jest nie lada wyzwaniem. Jeśli się powiedzie, to zadanie nie powinno juz sprawić kłopotu. Wypadałoby jeszcze dodać, że kolory działek są tylko ozdobnikiem, czyli nie mają z regułami nic wspólnego.
Jako rozwiązanie wystarczy podać sumę liczb na przekątnych, choć oczywiście opis rozszyfrowanych reguł będzie mile widziany.
Przykład
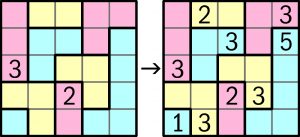
Zadanie
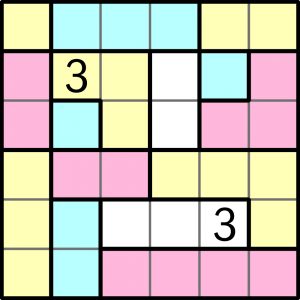
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Reguły produkcyjniaka:
(według: Jerzy Dobrowolski w „Czterdziestolatek”)
A – żylaste ręce
B – nagie torsy
C – twarde karki
D – poorane twarze
E – na tle nowej technologii
Do każdego wielokąta należy wpisać niepowtarzające się liczby z zakresu 1-N.
Celem jest utworzenie kwadratu łacińskiego.
Czy cyferki w polach mówią ile kroków trzeba zrobić z pola do kolejnego pola z cyferką?
Nie (aż tak ekstraordynaryjnie nie jest 🙂
mp
Ech, jednak nie taka reguła jak w moim drugim komentarzu.
Chyba poproszę o usunięcie.
Bo ujawnienie podpowiadałoby jakieś rozwiązania ?.
Pozostawiam decyzję Gospodarzowi.
Suma cyfr na przekątnych: 14
Oprócz reguł wstępnych dodatkowo:
– w każdej działce powinna znaleźć się tylko jedna cyfra
– puste pola powinny tworzyć spójny obszar (możliwy do objechania wieżą szachową).
– w każdym kwadracie 2×2 musi pojawić się co najmniej jedna cyfra oraz co najmniej jedno pole puste.
Trzeci warunek jest znacznie prostszy (dwa pozostałe są OK).
mp
I kiedy już miało być tak pięknie (zacząłem już być z siebie dumny i takie tam) to zobaczyłem jeszcze jedną trójkę na przekątnej.
Czyli suma = 17.
Socrealizm
Sprawiedliwie znaczy po równo, a jeżeli nie da rady po równo, to przynajmniej tak, aby zasobniejszych było jak najwięcej, a uboższych – jak najmniej i różnice między nimi – jak najmniejsze.
PS
Zasobniejszych, uboższych (wierszy, kolumn) w cyfry. Aby zabezpieczyć się przed donosem sygnalistki Reality o szerzeniu komunizmu, wprowadzamy zróżnicowanie – dodatkowy warunek maskujący – w żadnym wierszu i kolumnie cyfry nie mogą się powtarzać (nie mogą być sobie równe!).
Na przykład:
1 , x , 3 , x , x , 2
x , 3 , x , 2 , 1 , x
2 , 1 , x , x , x , 3
x , x , 2 , 4 , x , x
x , 2 , x , x , 3 , x
3 , x , 4 , x , x , x
1. Odpowiednia cyfra musi być wpisana na jednym z dwóch końców działki.
2. W rzędzie może być jedna lub dwie cyfry.
Mam taką teorię:
1. Fragment „kwadratu łacińskiego”
2. Dla każdych dwóch pustych komórek istnieje droga łącząca te komórki ruchem wieży szachowej
Tylko jeszcze nie sprawdzałem rozwiązania.
Warunek (2) – OK. Warunek (1) – osobliwy, bo fragmentów k. ł. mogłoby być ho, ho!
mp
Moja wydedukowana reguła jest taka, że kombinacje cyfr muszą być takie same w wierszach i w kolumnach (zachodzi dla przykładu), ale rozwiązanie nie jest unikalne (więc sumy na przekątnych też nie). No i klops.
Czy takie same cyfry nie mogą przylegać do siebie i nie mogą powtarzać się w rzędzie i kolumnie? Te reguły zostawiałyby jeszcze kilka stopni swobody.
Nieprzyleganie takich samych cyfr – tak:). Niepowtarzanie się w rzędzie (wiersz, kolumna) – nie):
mp
-W rzędzie i kolumnie 2 lub 3 cyfry
-Cyfra na końcu działki
-Cyfry nie powtarzają się w rzędach i kolumnach
-Jednakowe cyfry nie stykają się nawet rogiem
Na jednej przekątnej – 1, 3, 3, na drugiej 2, 1, 2.
Odp.: 17
1. Pola bez liczb muszą tworzyć spójny obszar.
2. Obszar ten nie może zawierać kwadratu 2×2.
3. Takie same liczby nie mogą dotykać się bokami.
Powyższe reguły pozwalają rozwiązać jednoznacznie przykład, ale brakuje im czegoś żeby rozwiązać większy diagram.
Proponuję jedną z dwóch poniższych reguł.
4a. Takie same liczby nie mogą dotykać się również rogami.
4b. Pola z liczbami nie mogą tworzyć kwadratów 2×2.
123456 / abcdef = 936666 / 669663
Tyle samo takich samych sum w wierszach i kolumnach.
?- to chyba powinno być pod innym wpisem. Jeśli tak, to proszę wpisać pod właściwym, bo ja nie mam możliwości przenosić komentarzy.
mp
19
13?
Deus ex machina.