Poślizg 2
Dziś jeszcze jedno zadanie poślizgowe, czyli takie, które wprawdzie liczbowo jest aktualne, ale byłoby aktualniejsze, gdyby pojawiło się u zarania bieżącego roku. To także powtórka z niedawnego „trzy-po-trzy”, choć nieco odmienna, bo bez ujawnionych wyników działań – poza jednym, ostatecznym.
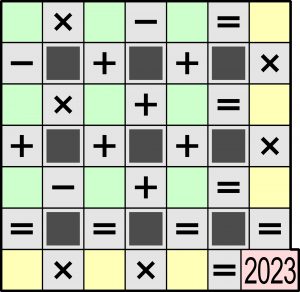
Przypominam: chodzi o wpisanie w zielone kratki dziewięciu różnych cyfr – od 1 do 9 – tak, aby równości w czterech wierszach i czterech kolumnach były poprawne (zatem jest to raczej „cztery-po-cztery”). Jak widać reguła ta dotyczy też nie ujawnionych (ale łatwych do ustalenia) wyników działań w sześciu rzędach, które stają się czynnikami prowadzącymi do finałowego tegorocznego iloczynu.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Wystarczy rozłożyć 2023 na czynniki (7,17,17), później jest łatwo
A B C D E F G H I
6 4 7 2 8 1 3 5 9
Miałem już przygotowany program do rozwiązywania takich zadań (napisany do zadania z wpisu „Sześć zer”), więc poszło szybko:
6 4 7
2 8 1
3 5 9
647
281
359
2023 = 7*17*17
7 może być sumą tylko w pierwszej kolumnie i w trzecim rzędzie, bo tam nie może być 17, maksymalna suma to 8+9-1 = 16.
Sposób rozwiązania polega na znalezieniu rozłącznych trójek, dających w sumie 17 (kolumny 2 i 3), tak żeby z pozostałych trzech liczb dało się złożyć 7. Są dwie takie pary trójek: (1, 7, 9) i (3, 6, 8) oraz (1, 7, 9) i (4, 5, 8). Tylko druga z nich daje rozwiązanie:
6 4 7
2 8 1
3 5 9
Jedyne rozwiązanie:
647
281
359
6×4-7=17
2×8+1=17
3-5+9=7
Fajnie było, rozterek co niemiara,
iloczyn pierwszy już zacząłem zrywać,
i tam, po zejściu pod podłogę,
przestało serce bić na trwogę.
6, 4, 7
2, 8, 1
3, 5, 9
(nie wiem, czy to jedyne rozwiązanie)
To chyba pierwsze tego typu zadanie, w którym zachowana jest kolejność działań, więc wyszło naprawdę elegancko!
No i jest proste, bo liczba 2023 jednoznacznie rozkłada się na 3 czynniki pierwsze.