Z poślizgiem
W poprzednim wpisie było zadanie, którego… nie było – we właściwym czasie, czyli na przełomie lat 2022 i 2023. Chodzi o łamigłówkę „trzy po trzy” z wynikami utworzonymi z kawałków liczb przypisanych słusznie minionemu i bieżącemu rokowi. Zamieszczając je przypomniałem sobie o innym przełomowym zadaniu również bezwzględnie pominiętym przed z górą czterema miesiącami i postanowiłem je także poniewczasie uczynić użytecznym. To tzw. dzielenie szkieletowe z ujawnionymi, choć nieco rozrzuconymi latami:
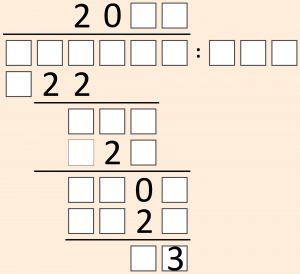
Większość cyfr w zapisie dzielenia zastąpiono kratkami. Korzystając z ujawnionych cyfr, należy rozszyfrować działanie. Szkielet jest trochę nietypowy, ze względu na występującą w nim resztę z dzielenia. Jest też trochę ułomny, ponieważ ma więcej niż jedno rozwiązanie. Aby miał jedno, zadanie należałoby uzupełnić następującym warunkiem dodatkowym: „w powyższym (rozszyfrowanym) zapisie dzielenia nie występuje cyfra …”. Właśnie, która, jeśli jest to cyfra parzysta?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Znalazłam dwa rozwiązania, z tym, że w obydwu nie występuje cyfra 4.
731820 : 361 = 2027 r. 73
529120 : 261 = 2027 r. 73
Czy to o to chodziło?
Niezupełnie. Wszak dodatkowy warunek o braku cyfry powinien być taki, aby rozwiązanie było jedno.
mp
Jedynym rozwiązaniem jest:
731820 = 2027 * 361 + 73
W pustych polach występują wszystkie cyfry prócz 4.
Pozostałe dwa ułomne rozwiązania to:
529120 = 2027 * 261 + 73 brak 3 i 4
326420 = 2027 * 161 + 73 brak 5, 8 i 9
Nie rozumiem. Przecież po podaniu warunku o braku cyfry 4 rozwiązania będą dwa.
mp
Jeżeli dodatkowy warunek będzie brzmiał: „…nie występuje TYLKO cyfra 4 (a pozostałe {0,1,2,3,5,6,7,8,9} występują)” to mamy jedno rozwiązanie (to pierwsze). Jeśli pominiemy słowo TYLKO to mamy 2 rozwiązania (pierwsze i drugie).
Czyżby nie było cyfry parzystej, której brakuje tylko w jednym zapisie rozwiązania?
mp
Jeśli tak na to spojrzeć to w trzecim rozwiązaniu brakuje 8 (oraz 5 i 9 ale to nas tu nie interesuje). Jednocześnie ta 8 występuje w pierwszym i drugim rozwiązaniu. A więc tak na to patrząc, to trzecie rozwiązanie jest właściwe. Jak widać mamy niespodziewane qui pro quo wynikające z subtelności językowych pozwalających na różne interpretacje intencji autora 🙂
Są trzy rozwiązania:
529120 : 261 = 2027 r. 73
731820 : 361 = 2027 r. 73
934520 : 461 = 2027 r. 73
Trzecie jako jedyne nie ma w zapisie dzielenia pisemnego 8, więc jest tym szukanym.
Dodatkowy warunek- „w powyższym zapisie dzielenia nie występuje cyfra 8.
326420:161=2027 reszta 73.
Cyfra 4 nie występuje w dzieleniach : 529120:261 oraz 731820:361=2027
Żałowałem, że odpuściłem podobne zadanie pod tytułem „słupek rzymski” z 1.04, więc tym razem postanowiłem jednak spróbować bez wsparcia komputera.
No i okazało się to całkiem zjadliwe zadanie na kartkę i długopis (i pod koniec również kalkulator)!
Jeżeli dodamy warunek, że w zapisie nie występuje cyfra 8, to jedynym rozwiązaniem będzie:
2027 : 161
A jeżeli tego warunku nie będzie, to dodatkowo:
2027 : 261
2027 : 361
Zapis rozumowania jest tu (brudnopis, ale myślę, że wiadomo, o co chodzi):
http://ersonasolidna.pl/lamiblog/20230506_Z_poslizgiem/2023-05-06_z_poslizgiem.jpg
326420:161 (brak 8)
529120:261
731820:361
@OlaGM
Trzecie Pani rozwiązanie wypada poza szkielet. Też się zorientowałem po jakimś czasie bo nie sprawdzałem dokładnie tych warunków 🙂