Droga numerowa
Instrukcje obsługi łamigłówek są z natury „dyktatorskie” – jest w nich o tym, co należy i czego nie wolno, a kto chce rozwiązywać, ten musi być posłuszny. Niektóre zakazy powtarzają się, a typowy dla wielu zadań, polegających na dzieleniu pokratkowanego diagramu na części, zabrania wydzielania kwadratu 2×2 kratki. Łamigłówką, w której ten zakaz ma specyficzną cyfrową formę jest nanro – dziełko wymyślone w roku 2000 w Japonii (nazwa jest skrótem wyrażenia „numerowa droga”). Przypomniałem sobie o nim, przeglądając zadania z tegorocznych 29 Łamigłówkowych Mistrzostwa Świata, które miały miejsce pod koniec października w Krakowie (Polacy wypadli blado, ale organizacja była na medal). Nanro pojawiło się w programie imprezy dwukrotnie, ale w Łamiblogu żadne z tej pary nie zagości, bo na publikacje zadań z Mistrzostw jest szlaban. Sięgnąłem więc do archiwum i wybrałem jeden z pierwszych niezbyt wyszukanych okazów, jakie rozwiązywali przed 22 laty Japończycy. Być może bardziej zakręcony będzie za tydzień.
Zasady zabawy są nieco zawiłe.
Do niektórych lub wszystkich pól każdej działki, na które podzielony jest diagram, należy wpisać liczby. Wszystkie liczby w danej działce powinny być jednakowe i powinno ich być tyle, jaka jest wartość każdej (jedna jedynka, dwie dwójki… itd). W sąsiednich polach (stykających się bokiem) nie mogą znaleźć się takie same liczby, jeśli pola te należą do różnych działek. Pola z liczbami muszą tworzyć jeden spójny wielokąt, nie zawierający kwadratu 2×2. Na początku kilka liczb jest ujawnionych.
Z lewej – mini przykład, z prawej – zadanie.
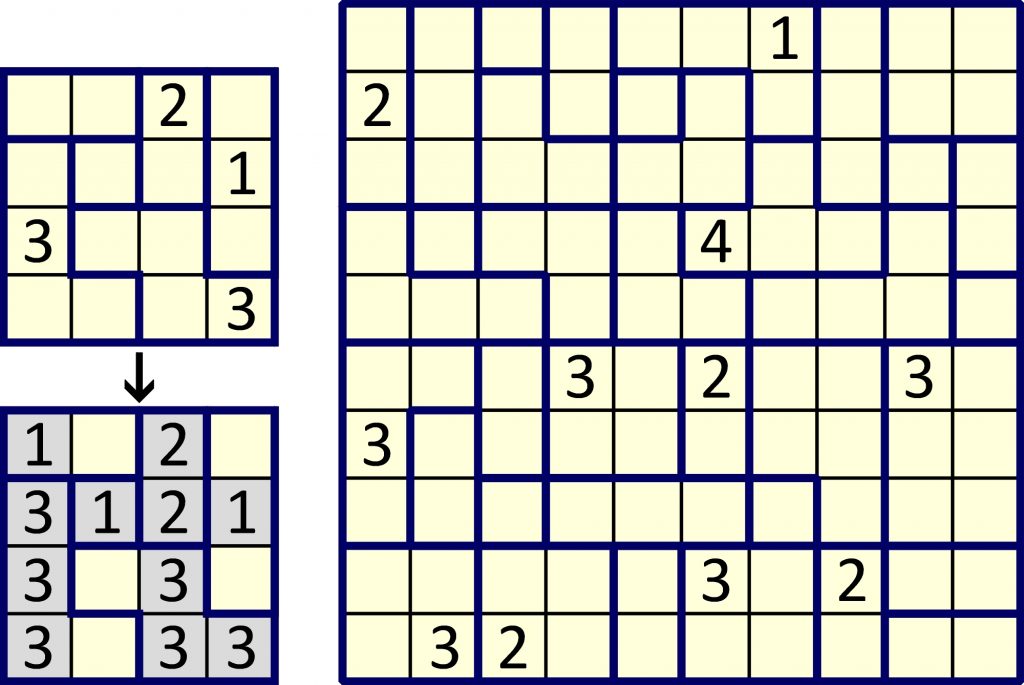
Jako rozwiązanie można podać sumę liczb na przekątnych.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Sumy na przekątnych 10 i 20 razem 30.
= = 1 2 = = 1 2 3 3
2 1 = 2 1 2 = 2 = 3
2 = 1 = 2 = 4 = 1 2
3 1 2 2 1 4 4 4 = 2
3 = 3 = = = 2 = 2 1
= 3 1 3 3 2 4 4 3 =
3 1 = 3 = 2 = 4 = =
3 = 1 2 2 = 1 4 3 3
= 3 = = = 3 = 2 = 1
3 3 2 2 1 3 3 2 1 =
Przekątna „\”: 1+1+2+2+4=10
Przekątna „/”: 3+3+1+3+3+4+3=20
https://images92.fotosik.pl/634/9d7c8f6e4751c070.jpg
Wydaje mi się, że jest to jedyne rozwiązanie, ale ta figura ma w środku (pola d6, e6, f6) dziurę, więc trochę naciągany z niej wielokąt. Liczy się?
Oczywiście. To wielokąt złożony.
No i znowu w niedoczasie:
Aż mnie korci, żeby skomplementować łamigłówkę, ale nie wiem, czy to wypada przed rozwiązaniem (troszkę mi jeszcze końcówka niedomaga, ale chcę ją tak bardziej na logikę a nie siłowo, więc to chwilę jeszcze potrwa).
Świetne zadanie.
Kiedy już Japończycy zrobią to, co trzeba, wtedy pochylę się nad tą końcówką.
Lubię tego typu reguły – prowadzą do ciekawych analiz – kiedyś już wspomniałem, że przypominają mi nostalgiczne „stawy i groble”- podtrzymuję i wzmacniam tę moją skromną opinię.
Suma liczba na przekątnych to 28.
Mam wątpliwość – jedynka może być na jednym z dwóch pól: g5 albo h4 – nie wpływa to na sumę kontrolną i może zostać przeoczone.
Trochę mnie Niemcy poganiają i być może mylę się.
Suma liczb na przekątnych wynosi 30 (na jednej 10, na drugiej 20)
10 i 20
Wpis @apartado mnie zmotywował, bo japońskie łamigłówki bardzo lubimy, ale też czasu ostatnio nie za wiele. Tylko szkoda że już jest odpowiedź (spróbujemy ją zignorować).
Pytanie: czy każda działka musi mieć jakieś liczby? Wygląda na to że tak, ale się upewnię.
Tak – każda działka musi zawierać przynajmniej jedną liczbę.
Rozwiązanie apartado jest unikalne – inne niż „oficjalne” zawarte w pozostałych komentarzach. Dlatego komentarze apartado uwalniam nieco wcześniej, aby był czas na ewentualne przedyskutowanie ich poprawności.
mp
https://zapodaj.net/124789dd16771.png.html
Na przekątnych jest suma 28.
Reszta też wygląda OK.
Dwie jedynki w kółkach mogą występować alternatywnie.
Co przegapiam ?
Gospodarzu – Mistrzu: help!!!
Szanowny Czeladnik przerósł Mistrza, bo grzechu nie widzę. Zatem są dwa (a nawet trzy) rozwiązania(?), choć wcześniej tego drugiego/trzeciego nikt nie znalazł.
mp
Wyszło 20+10=30. Trochę się połamigłówkowałam.
Zadanie fajne, żadnych stopni swobody, wszystko musi być przemyślane.
@Mistrz
Trójka g2 może znaleźć się też na g1.
Jedynki z pól g5,h4 też są dwupołożeniowe.
Są to zdarzenia niezależne, więc mnożymy 2×2=4.
Czyli zadanie ma 4 rozwiązania.
No chyba, że coś mylę poganiany przez wistość rzeczy.
Wyszło mi równo 30
Jedno rozwiązanie. Bez rozwidleń. Wystarczy rozważać najbliższe sąsiedztwa korzystając równomiernie ze wszystkich reguł, dlatego wzrost rozmiaru nie zwiększa trudności szybciej niż wrost powierzchni. Fajne zadanie. Napisanie programu dużo żmudniejsze niż ołówkiem. Suma przekątnych = 30.
https://foteczkowo.pl/ib/tod1D4r6Em
@apartado
W Twoim rozwiązaniu dwójka z przedostatniego wiersza stała się jedynką 😉
Wygląda poprawnie, ale zahardkodowana 2 w h2 (wg numeracji @apartado) zamieniła się w 1. Więc chyba nie jest to „dodatkowe” rozwiązanie.
Zadanie Marka ma jedno rozwiązanie. Apartado rozwiązał inną łamigłówkę.
Należy zwrócić uwagę na miejsce. w którym w oryginalnym zadaniu jest 2 a Apartado wpisał 1. Drugi wiersz od dołu i trzecia kolumna z prawej.
Znaczy, że dzisiaj (piątek, 2022-12-02, 23:38) nie będzie uwolnienia?
Macierewicz?
Jak się człowiek śpieszy to się diabeł cieszy.