Według Fujimury

7 maja 2022
Marek Penszko

W uchodzącej za klasyczną, wydanej po raz pierwszy w Japonii przed półwieczem książce Kobona Fujimury „Tokyo Puzzles” (tytuł angielskiego przekładu), jest zadanie w rodzaju łamigłówek trzy po trzy, które wygląda tak (oryginalny rysunek z książki):

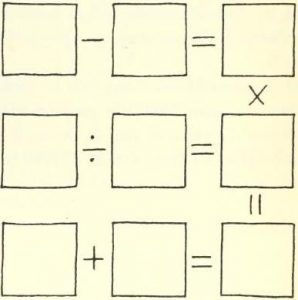
W kratki trzeba wpisać dziewięć różnych cyfr tak, aby wskazane działania w trzech wierszach i jednej kolumnie były poprawne. Zadanie jest proste. Można nawet poradzić sobie z nim „w głowie”, zważywszy, że możliwe mnożenia i dzielenia do rozpatrzenia są praktycznie tylko dwa parami „bliźniacze” i skrzyżować je można tylko na dwa sposoby. Co jednak istotniejsze – ten drobiazg jest inspirujący. Dlaczego autor nie pokusił się o ułożenie czegoś nieco ambitniejszego, czyli z działaniami we wszystkich kolumnach albo chociaż w jeszcze jednej, ale zachowując niepowtarzalność cyfr? Odpowiedź wydaje się oczywista – nie jest to możliwe. I drugie pytanie: a gdyby dodać zero, to czy sześć działań dałoby się utworzyć? Wydaje się, że także nic z tego, bo zero niewiele zmienia. Musi wystąpić w parze z jedynką jako 10. Ratunek stanowi zwiększenie zakresu wolności dla znaku równości. Inaczej mówiąc, nie zawsze musi być 3 – 1 = 2, bo czasem może być też 3 = 1 + 2, czyli działanie w wierszu lub kolumnie można zapisać jakby wspak – najpierw znak równości, a potem znak działania.
Pora więc na orzeszek: w kratki należy wpisać komplet cyfr w postaci dziewięciu liczb – od 2 do 10; a w kółka sześć znaków działań i sześć znaków równości. Oczywiście tak, aby działania działały jak należy.

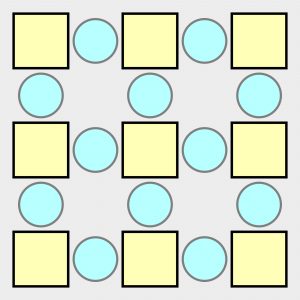
Ile różnych rozwiązań (z dokładnością do obrotów i odbić) ma to zadanie – tego nie wiem. Ale jedno na pewno.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.