Piąta kolumna
Cztery hetmany szykują się do opanowania piątej kolumny. Zaczynają: pierwszy ląduje na polu a3; po nim drugi zajmuje b8, następnie trzeci c4. Prawie wszystkie pola piątej kolumny – różowe na rysunku – są już opanowane.
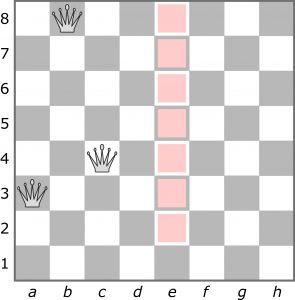
Teraz wystarczy, aby czwarty hetman zagościł na d1 lub d2 i będzie po sprawie.
Ile jest takich różnych ustawień czterech hetmanów na czterech pierwszych kolumnach (po jednym na każdej), po których wszystkie pola piątej kolumny będą atakowane? „Różnych” oznacza pominięcie odbić lustrzanych w pionie. Odbicia lustrzane w poziomie są dozwolone, bo „działają” inaczej; ustawienie 1483 jest więc inne niż przykładowe 3841.
PS (dopisane 20.02) hetmany nie mogą się wzajemnie atakować (przepraszam, zapomniałem).
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
58
Uwolnione ze względu na PS.
mp
Różnych rozwiązań jest 58.
Uwolnione ze względu na PS
mp
1: 1 4 6 3
2: 1 4 8 3
3: 1 6 2 7
4: 1 6 4 7
5: 2 7 3 8
6: 3 8 4 1
7: 3 8 4 2
8: 3 8 6 1
9: 3 8 6 2
Wszystkich ułożeń bez dodatkowego warunku z PS jest 58, to już wiemy.
Wśród nich tylko w 9 ustawieniach hetmany się nie atakują.
Zakładając, że hetman w pierwszej kolumnie znajduje się w rzędach 1-4, są to:
1463, 1483, 1627, 1647, 2738, 3841, 3842, 3861, 3862.
Wyszło mi 9.
d1, c4, b8, a3 = d8, c5, b1, a6
d1, c6, b2, a7 = d8, c3, b7, a2
d1, c6, b8, a3 = d8, c3, b1, a6
d2, c4, b8, a3 = d7, c5, b1, a6
d2, c5, b3, a8 = d7, c4, b6, a1
d2, c6, b8, a3 = d7, c3, b1, a6
d2, c7, b3, a8 = d7, c2, b6, a1
d3, c6, b4, a1 = d6, c3, b5, a8
d3, c8, b4, a1 = d6, c1, b5, a8
Jest 9 istotnie różnych rozwiązań w których hetmany się nie atakują wzajemnie. Rozwiązania można pogrupować w trzy pary i jedną trójkę. W parach rozwiązania różnią się małym przesunięciem tylko jednego hetmana o jedno lub dwa pola. W trójce jedno rozwiązanie jest bliskie dwóm pozostałym a te dwa pozostałe bliskie sobie nie są. Rozwiązanie „centralne” różni się od jednego z dwóch pozostałych, jak w poprzednich przypadkach małym shiftem jednego hetmana ale od drugiego różni się przesunięciem wszystkich hetmanów o ten sam wektor. Rysunek w linku poniżej:
https://zapodaj.net/6bed99e13a4fc.jpg.html
Jestem pewien, że układy Hetmanów są już dokładnie policzone, a więc (z cyklu wariacje na temat):
Na dowolnych polach znajdujących się na lewo od piątej kolumny należy rozmieścić pięć figur szachowych (po jednej):
Król,Hetman,Goniec Skoczek,Wieża
Warunki podstawowe:
1. Cała piąta kolumna powinna być szachowana.
2. Każda figura powinna być szachowana dokładnie jeden raz.
Warunek/cel dla wytrwałych:
3. Sumaryczna odległość figur od piątej kolumny powinna być jak największa.
H: a8
W: a6
G: b4
S: d3
K: d2
@Andrzej111
Piękny układ i nieźle punktowany – sumaryczna odległość figur od piątej kolumny to 13.
Żeby zmotywować do dalszej wytężonej pracy na odcinku dodam, że istnieje przynajmniej jedno rozwiązanie z punktacją 15.
@apartado
Zadanie mnie przerosło.
Nie tylko nie znalazłem rozwiązania dla sumy równej 15, ale nawet mniejsza wartość okazała się dla mnie nieosiągalna.
@Andrzej111
Poniżej dwa przykładowe układy dla których sumaryczna odległość od piątej kolumny to 15.
(15 to najprawdopodobniej maximum.)
#####
w####
h####
#####
g##k#
#####
##s##
#####
#####
s####
#####
#h#k#
#g###
w####
#####
#####