Blokersi sumują bis
Przedstawione w poprzednim wpisie małe blokowisko sumowe było proste. Chyba nawet prostsze niż jego pierwowzór z liczbami, określającymi nie sumę wysokości widocznych bloków, tylko ich liczbę. Na ogół jednak większe blokowiska z sumami są trudne i bardzo trudne, ponieważ w przypadku podania sumy liczb z reguły jest wiele możliwości ich rozmieszczenia, a przede wszystkim zwykle konkretnie nie wiadomo, ile tych liczb jest. Oczywiście, jeśli suma jest maksymalna, czyli np. 10 dla diagramu 4×4, to odpowiada to liczbie 4 w „klasycznym” zadaniu i dany rząd można natychmiast wypełnić cyframi (1-2-3-4); już jednak przy sumie 7 jest osiem siedem możliwości ustawienia czterech cyfr, a gdy wielkość diagramu wzrasta, sytuacja mocno się komplikuje.
Na szerszym forum pierwsze blokowisko z sumami pojawiło się na 12. Łamigłówkowych Mistrzostwach Świata w roku 2003 w Arnhem. Proponuję samemu przekonać się, że Tim Peeters zaoferował uczestnikom tej imprezy orzech sporej twardości.
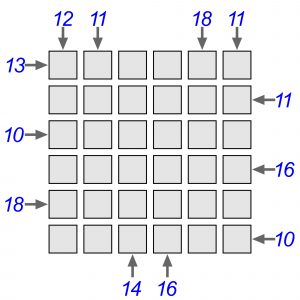
Jako rozwiązanie wystarczy podać ciąg sześciu liczb na przekątnej lewa góra-prawy dół.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
124635
536241
461523
645312
312456
253164
Można usunąć cztery liczby i rozwiązanie pozostanie jedno:
Góra – 12
Dół -14
Prawy bok – 11, 10
Czy ja wiem, moim zdaniem nie było trudne. Za to bardzo przyjemnie się rozwiązało podczas nudnej podróży autobusem!
Na przekątnej mamy 131354.
1,3,1,3,5,4
131354
Przyjemne 🙂
131354 – ok. 35 minut
Pozdrawiam,
Przekątna:
1 3 1 3 5 4
131354
Dla planszy o boku 4 potrzeba nie więcej niż 3 wskazówki, żeby jednoznacznie zdefiniować rozwiązanie.
Ciekaw jestem ile ich minimalnie potrzeba dla rozmiaru 6 ?.
12 wygląda na oko na „o wiele za dużo”.
A może gdzieś w OEIS znajduje się już uogólniona odpowiedź? – nie zdziwiło by mnie to.
Dla diagramu 4×4 i sumy 7 możliwości jest siedem a nie osiem:
1243
3124
3214
3142
3241
3412
3421
7 jest sumą dającą najwięcej możliwych układów. Jeszcze tylko dla sumy 4 możliwości jest sześć, a dla wszystkich innych nie więcej niż trzy. A w klasycznym blokowisku, przy dwóch widocznych blokach możliwości jest 11.
W klasyce przy dwóch widocznych blokach zawsze jest najwięcej możliwości – niezależnie od wielkości blokowiska. Jak to jest z sumami? – oto zagadka.
Niezależnie od liczby możliwości układ z sumami jest (moim zdaniem) bardziej „zakręcony”, czyli trudniejszy do analizowania.
mp
Zaryzykowałbym stwierdzenie, że dla diagramu NxN najwięcej możliwości mamy dla sumy równej 2N-1.
Ale głowy za to nie daję 😉
131354
Do apartado: zgadzam się z tą hipotezą. Najwięcej jest dla 2N-1, a na drugim miejscu dla N – tu jest to zawsze (N-1)!
Dla 5×5 suma 9 ma 27 możliwości
Dla 6×6 suma 11 ma 142 możliwości
Dla 7×7 suma 13 ma 834 możliwości
Dla 8×8 suma 15 ma 5962 możliwości
Odpowiedniego ciągu w OEIS brak,ale prawdopodobnie będzie to suma jakichś ciągów tamże obecnych.
Dla klasycznego blokowiska odpowiedni ciąg tworzą tzw. liczby Stirlinga I rodzaju (pozbawione znaków).
mp
Dla diagramu o boku N=6 mamy:
suma 6 mozliwości 120
suma 7 mozliwości 24
suma 8 mozliwości 30
suma 9 mozliwości 46
suma 10 mozliwości 68
suma 11 mozliwości 142
suma 12 mozliwości 41
suma 13 mozliwości 53
suma 14 mozliwości 50
suma 15 mozliwości 73
suma 16 mozliwości 23
suma 17 mozliwości 17
suma 18 mozliwości 23
suma 19 mozliwości 4
suma 20 mozliwości 5
suma 21 mozliwości 1
Najwięcej możliwości widać przy sumie 2N-1
2*6-1 czyli suma 11 daje 142 możliwości.
Ponadto można zauważyć dwa „maksima wtórne” przy sumach równych N oraz 3N-3, czyli mamy także dużo możliwości przy sumie 6 (120) i 15 (73).
Analiza dla diagramów o innych rozmiarach (N= 4,5,7,8) potwierdza wzory na te trzy maksima.
1;3;1;3;5;4
Super! Tak mnie wciągnęło dziś po pracy, że musiałem skończyć. Mocne ale bez zgadywania – czysta dedukcja. Właściwie Blokersi to odległa wariacja na temat Sudoku, co ja nazywam Cudaku. Sumersi blokują!
Liczbę możliwości dla 3 najmniejszych sum opisują proste wzory:
(n-1)!
(n-2)!
(n-2)!+(n-3)!
Z kolei dla 5 sum największych mamy (jadąc od końca):
1
n-1
n-2
n^2-2n-1
n^2-3n-1
Dla innych już tak prosto nie jest
131354
Gdy się już opracuje strategię rozwiązywania, to idzie szybko. Warto wypisać rozkład każdej liczby z uwzględnieniem 6. Wcale dużo tego nie jest, np. w przypadku 10 mamy jedynie 136 i 46; w przypadku 11 mamy tylko 146, 236 i 56 itd. (Nawet jeśli rozkładów jest więcej niż trzy, to szybko się potem redukują).
Następnie warto w pierwszym polu przy każdej liczbie wpisać opcje, np. przy 10 wpisujemy 14, przy 11 wpisujemy 125 itd. A potem to już prawie jak sudoku (wiem, że prawie robi dużą różnicę). W każdym razie jakiś bardzo twardy orzech to nie był.
Tak „na oko” wydaje mi się że ilość możliwości dla sumy to nie jest dokładnie to samo co trudność analizy danego rzeędu (nie mówiąc już o diagramie)
Na przykład suma 6 daje jednoznaczne położenie 6-ki, sumy powyżej 11-tu dają informację że 5-ka jest przed 6-ką. Dla niektórych sum, można wykluczyć widoczność liczb (np: dla sumy 10 na pewno nie widać 2 i 5)… Często widocznośc i kolejność liczb daje więcej informacji niż ilość możliwości.
Stąd więc (nie poparte dowodem) twierdzenie 🙂
Pozdrawiam,
Jednoznaczne rozwiązanie dla tego diagramu jest po usunięciu każdej sumy z wyjątkiem trzech: obu 11 na górze i 16 z prawej strony. W każdym z tych trzech przypadków usunięcie jednej sumy powoduje, że zamiast jednego są dwa rozwiązania.
@tomash
Nie zawsze dla sumy powyżej 11 mamy pewność, że 5 jest przed 6.
Przykład: 246135 (suma 12, patrzymy oczywiście z lewej).
Wygląda na to, że można usunąć 4 sumy (12 i 18 u góry oraz obie 10) i nadal będzie jedno rozwiązanie
1 3 1 3 5 4
Komentarz trochę spóźniony, ale lepiej późno niż wcale. Chciałem tylko zwrócić uwagę, że sam problem szukania składników sumy jest bardzo popularnym zagadnieniem o praktycznym znaczeniu i nazywa się „problemem sumy podzbioru” (subset sum problem), który z kolei jest przypadkiem szczególnym problemu plecakowego (knapsack problem).
Jest całe mnóstwo rozważań matematycznych jak i informatycznych, a także gotowych rozwiązań – algorytmów w różnych językach programowania, a ja sam wiele lat temu natknąłem się na świat tych problemów musząc w pracy napisać algorytm znajdujący liczby, które w jakimś raporcie mogłyby się składać na zadaną, zagregowaną kwotę.