Antymagicznie
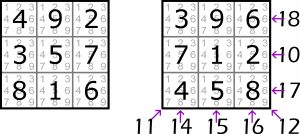
Kwadratowa antymagia była już w Łamiblogu na tapecie, ale przed wielu laty, więc nie zaszkodzi do tematu powrócić. Najczęściej kwadraty antymagiczne składają się z 9 pól (3×3), w których liczby od 1 do 9 rozmieszczone są tak, że wszystkie osiem sum trzech liczb – w trzech wierszach, trzech kolumnach i na dwóch przekątnych – jest różnych. To przeciwieństwo magii, gdy wszystkie te sumy są jednakowe – równe 15. Kwadrat magiczny 3×3 jest jeden (na rysunku z lewej strony), kwadratów antymagicznych tego formatu jest 3120 (przykład z prawej strony) – w obu przypadkach z dokładnością do obrotów i odbić lustrzanych.
Utworzenie jakiegoś kwadratu antymagicznego to przy ich obfitości zadanie bardzo proste. Trudniej zrekonstruować jakiś konkretny kwadrat, na podstawie podanych sum tercetów liczb. Poniższe zadanie tego typu pochodzi z łamigłówkowych mistrzostw Japonii, ale jest nieco zmienione.
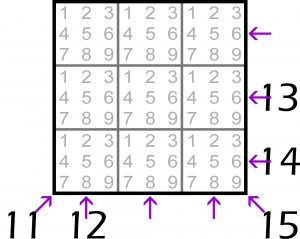
W oryginale podane było wszystkie osiem sum. Tutaj trzy sumy zostały usunięte – pozostało pięć będących kolejnymi liczbami, od 11 do 15, określających sumy liczb w dwóch wierszach, jednej kolumnie i na obu przekątnych. Mimo trzech braków rozwiązanie nadal jest jedno, choć znaleźć je niełatwo. Jeszcze trudniejsze jest dodatkowe pytanie: czy usunięcie jeszcze którejś z pozostawionych pięciu sum zawsze spowoduje pojawienie się większej liczby rozwiązań, czyli możliwych przynajmniej dwóch różnych rekonstrukcji kwadratu antymagicznego?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
5,6,7
4,1,8
3,2,9
567
418
329
Usunięcie dowolnej z pozostałych sum powoduje powstanie więcej niż jednego rozwiązania.
11)
279
481
635
12)
963
418
725
13)
153
967
248
14)
596
427
318
15)
963
274
158
Dodatkowe rozwiązania nie wyczerpują wszystkich innych rozwiązań, są tylko przykładami.
Jedyny kwadrat antymagiczny dla ww. warunków
5 6 7
4 1 8
3 2 9
Jeśli odpuścimy warunek na sumę a4+a5+a6, tutaj =13, to rozwiązanie antymagiczne będzie jedyne:
5 8 7
4 1 6
3 2 9
567
418
329
Mam nadzieję, że nie popełniłem jakichś głupich błędów podczas pisania programu… Oto moje ustalenia:
Rozwiązanie zadania jest faktycznie jedno:
5 6 7
4 1 8
3 2 9
Pozostałe sumy to 9, 18 i 24, mamy więc osiem różnych sum.
Co ciekawe, nie jest tu istotne założenie, że cały kwadrat jest antymagiczny! Gdyby zadanie brzmiało „uzupełnij kwadrat cyframi od 1 do 9 tak, aby podane sumy się zgadzały”, powyższe rozwiązanie nadal jest jedyne!
Co do usuwania sum: po usunięciu którejkolwiek z sum 11, 12, 14 i 15, pojawiają się dodatkowe antymagiczne rozwiązania. Natomiast po usunięciu 13, pojawia się pięć nowych możliwych wypełnień kwadratu cyframi od 1 do 9 (tak, aby sumy się zgadzały), ale tylko rozwiązanie oryginalnego zadania jest kwadratem antymagicznym. Tak więc można usunąć 13 i dalej mamy jedyność rozwiązania!
5 6 7
4 1 8
3 2 9
Łatwo jest pokazać, że następujące warunki są konieczne:
’14’ – zamiana 6 z 2 to drugie rozwiązanie
’12’ – zamiana 4 z 8 to drugie rozwiązanie
’11’ – zamiana 6 z 7 to drugie rozwiązanie
’15’ – zamiana 2 z 9 to drugie rozwiązanie
’13’ wygląda nie do ruszenia więc (chyba) jest zbędna.
Można usunąć jedną z sum: 13 albo 14, jednak w zamian musi być sprawdzona pominięta, ale znana suma z wiersza pierwszego: 18 (bo 45-13-14=18).
1)
Uśmiechnąłem się na widok rozwiązania.
5 , 6 , 7
4 , 1 , 8
3 , 2 , 9
2)
Usunięcie którejkolwiek z sum daje więcej rozwiązań.
Na przykład brak 11-ki generuje dodatkowo 13 rozwiązań.