Pib vs ms
Poprzedni wpis i umieszczone pod nim niektóre komentarze skłoniły mnie do krótkiej refleksji ogólnej na temat łamigłówek. Nie jest ona zbyt odkrywcza, dotyczy bowiem próby odpowiedzi na pytanie, kiedy rozwiązywanie łamigłówki jest rozrywką, a kiedy przestaje nią być, czyli staje się mniej lub bardziej żmudnym zajęciem albo – mówiąc oględniej – jest rozrywkowe inaczej?
Odpowiedź wydaje się prosta: decyduje o tym udział w sposobie rozwiązywania metody prób i błędów. Niektórych, zwłaszcza początkujących główkołamaczy irytuje, gdy już na starcie trafiają na pib – to sprawia, że często po prostu rezygnują z zabawy. Innych korzystanie z tej metody nie zniechęca nawet, gdy jej udział jest dominujący. Pomijam okoliczności związane z jakimś szczególnym bodźcem, gdy np. nagrodą za rozwiązanie jest milion funtów, jak w przypadku układanki Eternity z roku 1999.
Przypominam zamieszczone w poprzednim wpisie zadanie:
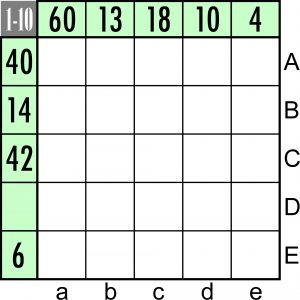
Do dziesięciu pól diagramu należy wpisać dziesięć różnych liczb – od 1 do 10. W każdym wierszu i w każdej kolumnie powinny znaleźć się dwie liczby – takie, aby ich suma lub iloczyn był(a) równy(a) wartości podanej przed wierszem lub nad kolumną z daną parą liczb (jeden wynik nie jest podany).
Zadanie było z założenia trudniejsze od jego prostszej wersji, w której wszystkie wyniki są iloczynami, ale w komentarzach przeważała opinia, że różnica stopnia trudności jest znikoma. Właściwie to mnie nie dziwi, bo przy odrobinie spostrzegawczości i logiki rozwiązywanie idzie jak po sznurku. Kolejno wpisywane są jako jedyne możliwe cyfry i ich miejsca: 6–aC, 7–dC, 2–cE (w wierszu E nie może być pary (1, 5), bo wtedy 2 znalazłoby się w dD i dla 9 nie byłoby miejsca w kolumnie d), 3–dE, 1–eD. Teraz pozostają do rozlokowania liczby 4, 5, 8, 9, 10, ale w wierszu A dla obu cyfr pary (5, 8) pasuje tylko jedno pole (bA), więc w tym wierszu musi się znaleźć para (4, 10). Ciąg dalszy to czysta formalność.
Załóżmy jednak, że nie zauważylibyśmy powyższej prostej drogi do celu, uznając, że jedyną możliwością jest pib. Alternatywę w takim przypadku stanowi odpowiednik komputerowej metody siłowej (ms) – skuteczny i prosty, ale schematyczny, wręcz sztampowy, więc jak na łamigłówkę przynajmniej nieelegancki, no i dość żmudny. Wyjaśnię, na czym w tym przypadku ms polega, choć zapewne większości Łamiblogowiczów nie trzeba tego wyjaśniać.
Wypisujemy przy każdym wierszu wszystkie możliwe pary liczb, które mogą się w nim znaleźć. Potem wybieramy pięć par – po jednej z każdej porcji, odpowiadającej danemu wierszowi – ale tak, aby w tych pięciu parach znalazło się dziesięć różnych liczb. W ten sposób otrzymujemy konkretne pary przyporządkowane określonym wierszom. Następnie robimy to samo dla kolumn, otrzymując pięć par liczb przynależnych kolumnom. Ustalone w ten sposób „współrzędne” jednoznacznie wyznaczają miejsce każdej liczby na przecięciu danego wiersza i kolumny.
OlaGM nadesłała w komentarzu następujące zadanie:
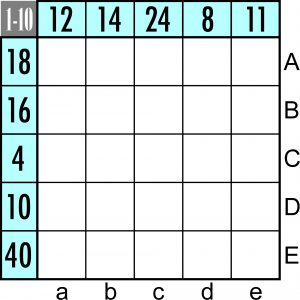
Można je oczywiście rozwiązać metodą pib, ale to raczej masochistyczne. Można też skorzystać z ms, ale to dłubacki schemat, któregom nie godzien. Czy jest na to zadanie jakiś sposób ps (po sznurku)? Wydaje mi się, że takowego nie ma, ale może się mylę.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Nawiązując do „Omnibusa” wspomnianego przez Pana Gospodarza:
Zadania o nazwie „Pantropy” spotkały się z BARDZO pozytywnym odbiorem społeczeństwa.
Zacytujmy z pamięci kilka głosów:
– „Świetne – nigdy się z czymś takim nie spotkałam!”
– „No wreszcie mamy kapitalne połączenie uwielbianej przeze mnie Jolki i krzyżówki panoramicznej ”
– „Dla mnie bomba – ciekawe czy Madzi też się spodoba?”
🙂 Dla mnie to zaskoczenie. Nawet podejrzewam ironię, bo nic nowego nie wymyśliłem.
mp
Zadanie super, znacznie trudniejsze od poprzednich!
Na początku wypisałem wszystkie możliwe pary liczb dla każdego wiersza i każdej kolumny, po czym wykluczałem pary przez dochodzenie do sprzeczności. Na przykład, w pierwszym wierszu nie może być para (8,10), gdyż to by wykluczało obie pary dla ostatniego wiersza, (4,10) i (5,8). Podobnie w wierszu czwartym nie możemy mieć par (1,9) i (1,10), bo jedynka musi być w wierszu trzecim, itd.
Dość łatwo można ustalić właściwe pary dla wierszy. Dla kolumn logika jest podobna, ale musi czasem sięgać głębiej, gdyż mamy tu więcej przypadków do rozpatrzenia.
Po jakimś czasie można już wpisywać konkretne liczby do diagramu, otrzymując jedyne rozwiązanie:
2 9 _ _ _
10 _ 6 _ _
_ _ 4 1 _
_ _ _ 7 3
_ 5 _ _ 8
Wyszło tak:
29xxx
10x6xx
xx41x
xxx73
x5xx8
Spodobała mi się idea metody siłowej, więc zacząłem od niej, w trakcie jednak posiłkowałem się metodą prób i błędów, bo tak całkiem po sznurku nie wychodziło. Podział na pięć par nie jest bowiem oczywisty, coś trzeba założyć, aż dojdzie się do sprzeczności, i od nowa.
Zacząłem od ograniczeń na wiersze 40, 4, 18 i kolumnę 24 i reszta się ułożyła.
2,9,_,_,_
10,_,6,_,_
_,_,4,1,_
_,_,_7,3
_,5,_,_,8
Jedyne rozwiązanie – metoda siłowa – program:
[2, 9, 0, 0, 0]
[10, 0, 6, 0, 0]
[0, 0, 4, 1, 0]
[0, 0, 0, 7, 3]
[0, 5, 0, 0, 8]
Nie wiem czy to się wpasowuje w pib, ms czy ps, ale:
1) w wierszu E może być 4×10 lub 5×8, a zatem w wierszu A nie może być 8+10, musi być iloczyn 2×9 lub 3×6
2) w wierszu C musi być 1, bo 4 = 1×4 albo 1+3
4) jeśli w wierszu E byłoby 4×10, to w C byłoby 1×3, pozostają cyfry 256789, czyli w A 2×9 i w B się nic nie da, a zatem w E 5×8, a w B suma 6+10 lub 7+9
5) jeśli w wierszu A byłoby 3×6, to w wierszu B 7+9, zatem w C 1×4, dla D pozostaje 2 i 10 – sprzeczność – zatem w A 2×9
6) Mamy A 2×9, B 6+10, C 1×4, D 3+7, E 5×8
7) W kolumnie c musi być iloczyn 3×8 lub 4×6. W kolumnach a i b nie mogą być jednocześnie iloczyny (3×4 i 2×7), bo nie dałoby się zrobić kolumny c.
8) załóżmy, że w b jest iloczyn 2×7, wtedy w a musi być suma 3+9 (4+8 wyklucza kolumnę c), wtedy w c 4×6, pozostają 158 i 10 i nie da się ułożyć kolumn d i e razem. A zatem w b jest suma – jedyna możliwa to 5+9, czyli mamy pola Ab i Eb.
9) w kolumnie a jest możliwe tylko 2×6 lub 2+10, a zatem w polu Aa mamy 2
10) Pola Ac, Ad, Ae, Bb, Cb, Db, Ca, Da, Ea są puste
11) w wierszu C 4 może być tylko w kolumnie c lub e (w d wyklucza 2 w Aa). Jeśli byłaby w Ce, to w De musi być 7. W związku z tym w kolumnie c musi być 3×8 i w kolumnie d 1×8 – sprzeczność. A zatem 4 w Cc.
12) 6 w Bc, 10 w Ba, 7 w Dd, 3 w De, 8 w Ee, 1 w Cd.
Trochę pib, trochę ms, ale w sumie całkiem przyjemnie się robi 🙂
Pozdrawiam,
MK
Dróżka do celu nie prosta, ale całkiem ładna, bo logiczna.
mp
,2,9,x,x.x
10,x,6,x,x
,x,x,4,1,x
,x,x,x,7,3
,x,5,x,x,8
2\9\x\x\x
10\x\6\x\x
x\x\4\1\x
x\x\x\7\3
x\5\x\x\8
W środkowym wierszu może być tylko (1,3) lub (1,4). Jedynka może być tylko w 4 lub w 5 kol. W wierszach muszą być przynajmniej dwa iloczyny, w kolumnach 1. Po 1 próbie ustawienia 1 (co mi się udało) dalej poszło jak z …
W wierszu C – 1,3 lub 1,4. To pierwsze nie brzmi najlepiej, wybiorę 1,4. Logiczne.
Skoro w wierszu C-czwórka, to w wierszu E – 5,8. W wierszu E nie ma 10-ki, mogłaby być w A lub B, ale w A nie będzie, bo gdyby była, to razem z 8, a wtedy w E nie byłoby nic, więc 10 musi być w wierszu B i na dodatek z 6. Skoro 10 i 6 już zajęte (przez B), w wierszu A może być tylko 2,9. Na placu pozostały liczby 3,7 oraz wiersz D, czyli – one z nim.
A = 2,9
B = 6,10
C = 1,4
D = 3,7
E = 5,8
Tak się zmęczyłem logicznym wywodem, uff!, że zamarzyłem o odrobinie niefrasobliwości (logiczne – bądź asertywny!). Wpiszę do kwadratu co upichciłem, a dalej się zobaczy, pokombinuję i może mi się trafi.
Ale jest warunek: w każdym wierszu i kolumnie po dwie liczby. To akurat daje się zautomatyzować (ach te logiczne maszyny!). Wpiszę po kolei od lewej do prawej, z góry do dołu, tak jak się czyta (logiczne), ustawiając schodkowo w pionie. Aby nie faworyzować którejkolwiek, najpierw mniejsza później większa.
W pierwszym wierszu 2,9 (aA,bA), w drugim 6,10 (bB,cB), w trzecim 1,4 (cC,dC), w czwartym 3,7 (dD,eD). W piątym 5,8 (eE, ?), ups!!? – nie mieści się! Wyłazi poza kwadrat, ale w pierwszej kolumnie jest miejsce (aE), w sam raz na 8.
2, 9, x, x, x
x, 6,10, x, x
x, x, 1, 4, x
x, x, x, 3, 7
8, x, x, x, 5
Jaki ciekawy widok, coś mi przypomina. W tamtym dominował jeden nad wieloma, tutaj jeden osaczony przez dwie linie gońców. Przyznam, żaden z tych schematów nie budzi mojej sympatii, ale nic nie poradzę, że cały świat znajduje w nich upodobanie, a nawet mówi że niczego lepszego nie wymyślono. Logiczne. Z logiką nie ma dyskusji. Jedziemy dalej, w tej konwencji muszę się zmieścić, coś przestawię, zamienię miejscami i będzie gites.
Srodkowa kolumna (c) zwraca uwagę: 4*6=3*8. Mogę ją uzyskać zamieniając miejscami 6 z 10 oraz 1 z 4 (4*6=24). Prawą kolumnę (e) zrealizuję przez zamianę 3 z 7 oraz 8 z 5, wynikiem 8+3=11. No proszę, przy okazji wyklarowała się kolumna (d) 1+7=8. Pierwsze dwie kolumny z lewej (a,b) zabłysną po zamianie miejscami 10 i 5, ale uwaga: liczby zmieniają kolumny ale nie wiersze.
2, 9, x, x, x
10,x, 6, x, x
x, x, 4, 1, x
x, x, x, 7, 3
x, 5, x, x, 8
Poszło jak po sznurku. Zaraz, zaraz!!! Na początku przyszło mi do głowy, że mam pewniaka: 1 na polu dC lub eC. Zupełnie o nim zapomniałem – a co z nim teraz się dzieje?! Jest! Na polu dC, co za ulga. Jest tam gdzie miał być. No i wszystko się dobrze skończyło.