Ciapa

15 sierpnia 2020
Marek Penszko

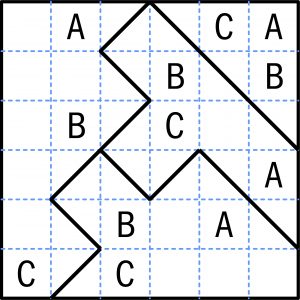
Podziel poniższy diagram na cztery części tak, aby w każdej znalazły się trzy różne litery.

Gdyby na podanym objaśnieniu poprzestać, rozwiązań byłoby mnóstwo. Intuicja podpowiada, aby dzielić wzdłuż boków kratek, czyli oznaczonych linii przerywanych, ale to niewiele zmienia. Natomiast japoński pomysł na uzupełnienie instrukcji jest genialnie prosty: dzielić należy wzdłuż przekątnych kratek, wtedy dzielenie, czyli rozwiązanie będzie jednoznaczne:

Tego rodzaju zadanie o przydługiej nazwie surasshupakku, którą można przetłumaczyć jako „ciachaj paczkę” (w skrócie „ciapa” 🙂 ), debiutowało w roku 2007 na łamigłówkowych mistrzostwach Japonii. Ze względu na nietypowy sposób cięcia uznane zostało za najbardziej oryginalne nie tylko na tej imprezie. Gwoli ścisłości wypadałoby dodać, że bokami wyciachanych części muszą być całe przekątne (i ich wielokrotności), czyli podział nie może zawierać kratek z takimi jak poniżej fragmentami linii dzielących:

Kolej na ciapę domową:

Tym razem chodzi o podział na cztery części z pięcioma różnymi literami w każdej. Ostrzegam, że łamigłówka jest nieco podstępna. W rozwiązaniu wystarczy podać „ilokątami” są poszczególne części (w podanym wyżej zadaniu przykładowym jest trójkąt i trzy ośmiokąty).

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.