Na ukos
Bazę zdecydowanej większości zadań diagramowych stanowi diagram w kratkę, zaś „nadbudów” określających ogólny rodzaj łamigłówki jest kilka. Jeden z tych rodzajów polega na dzieleniu diagramu – z reguły wzdłuż boków kratek, ale nie zawsze.
W ósmym Omnibusie (lato 2015) znalazły się zadania nazwane „Wycinankami”. Fragmenty boków wielokątów, na które należało podzielić diagram, były w nich ujawnione, a były to wszystkie boki ukośne leżące na przekątnych kratek. Rozwiązywanie sprowadzało się do dorysowania boków poziomych i pionowych, tradycyjnie wzdłuż boków kratek – tak, aby doprowadzić do pełnego podziału na części jednakowej wielkości – każda powinna składać się z 4 kratek. Oto przykład:
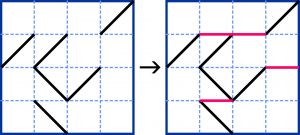
Pojawił się wówczas pomysł odwrotnego wariantu zadania, w którym ujawnione byłyby boki poziome i pionowe, a dorysować należałoby ukośne. Powyższy przykład po „odwróceniu” wyglądałby wówczas tak:

Nietrudno sprawdzić, że teraz przykładowe rozwiązania są trzy. Aby było jedno przykład powinien być inny, np. taki:
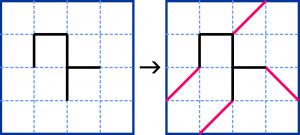
Kolej na zadanie polegające na dorysowywaniu ukośnych boków wzdłuż przekątnych kratek w celu podzielenia diagramu na dziewięć 4-kratkowych części (wszystkie boki poziome i pionowe są oczywiście ujawnione).

Zadanie ma więcej niż jedno rozwiązanie. Ile konkretnie?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Znalazłam niby dwa, ale ten drugi wariant ma chyba feler; zaznaczyłam go znakiem zapytania.
https://www.fotosik.pl/zdjecie/e9b7b2c74b0977c0
Jest OK, a feleru nie ma (wystarczy obrócić ukośną kreseczkę).
mp
Dwa rozwiązania
Jedno rozwiązanie znalazłem dość sprawnie.
Drugie „zmutowałem” na szybko – różnice w kratkach c2 i c3.
Więc chyba są dwa rozwiązania, bo nie widzę innych „mutacji”.
Widzę dwa rozwiązania. Tu jedno:
https://tiny.pl/75pch
Drugie powstaje przez obrót przekątnych na dwóch polach: c2 i c3.
Mi wychodzą tylko 2 rozwiązania.
Znalazłam dwa rozwiązania, które w większej części pokrywają się:
ukośne boki znajdują się w tych samych kratkach i tylko w dwóch przebiegają inaczej (wzdłuż drugiej przekątnej), a mianowicie w 2 i 3 kratce licząc od dołu w 3 kolumnie od lewej strony.
2
Zadanie niełatwe.
https://www.fotosik.pl/zdjecie/e8fa0f7fe48aac26
Proszę o powtórzenie komentarza pod właściwym wpisem. Zamieszczony został pod wpisem „Na ukos”, a dotyczy wpisu „Ciapa”. Ja nie mam możliwości przekierowania go we właściwe miejsce.
mp
Lewy (czerwony) wariant OliGM ma 4 lokalne mutacje (5,3) i (2,6).
Drugi (niebieski) ma te same 4 mutacje.
Ten drugi wariant można inaczej dokończyć w 5 i 6 kolumnie z 16 lokalnymi mutacjami. Dwie jak wyżej oraz (4,5) i (4,6).
@Spytko z Melsztyna
Ujawnione kreski poziome i pionowe to boki poszukiwanych wielokątów. Każdy ma być elementem linii łamanej zamkniętej.
@mag
Rzeczywiście , jeśli zdelegalizujemy sterczenie zbędnych odcinków to są tylko dwa rozwiązania. Przyjąłem, że te odcinki mogą ale nie muszą być bokami wielokątów 🙂