Qlisko

Komu nie obce jest zadanie zwane blokowiskiem, ten od razu zauważy, że dzisiejsze qlisko jest jego formalną odmianą. Zdecydowałem się na tę abstrakcję ze względu na bardziej wyraziste przedstawienie zasady widoczności obiektów na diagramie.
W polach diagramu należy rozmieścić kule różnej wielkości – o średnicach 1, 2, i 3 – tak, aby w każdym rzędzie znalazły się trzy kule o różnej średnicy, a jedno pole pozostało puste (zerowe). Liczba obok wiersza lub kolumny oznacza, ile kul widać w danym rzędzie, patrząc z miejsca, w którym jest liczba, w kierunku wskazanym przez umieszczoną obok niej strzałkę. Oczywiście większe kule zasłaniają mniejsze.
Gwoli jasności przykład:

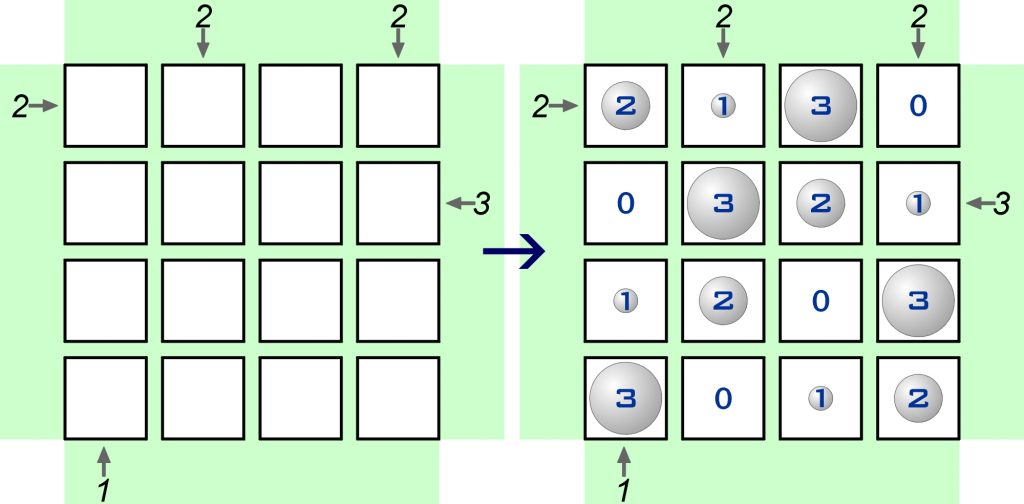
A zadaniem jest… tenże przykład (lewy diagram) po małej zmianie reguł.
Tym razem liczba także oznacza, ile kul widać w danym kierunku, ale nie spoza diagramu, tylko z pola zerowego w danym rzędzie (obserwator stoi na polu zerowym plecami do liczby).
Zaś pytanie brzmi: ile najwięcej kluczowych liczb (i które) można (należy) usunąć w przykładzie, aby miał on dokładnie jedno rozwiązanie?
Łatwo sprawdzić, że z oznaczonymi pięcioma liczbami rozwiązywanie prowadzi do sprzeczności.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[logi]

Gdy usuniemy „1” wskazujące pierwszą kolumnę i „2” wskazujące drugą kolumnę, to otrzymamy jedno rozwiązanie:
0132
3210
2301
1023

[xswedc]

Znalazłem rozwiązanie z usuniętymi dwiema cyframi: dolną jedynką i górną, lewą dwójką:
https://ifotos.pl/z/qqpaann

[xswedc]

Zgłaszam formalny protest. 🙂  Myślę, że zadanie ma zawsze dwa rozwiązania.

1. kiedy czytamy objaśnienie tak:
{liczba także oznacza, ile kul widać w danym kierunku}, ale nie spoza diagramu, tylko z pola zerowego w danym rzędzie
to liczba ma tylko jedno znaczenie (o które Panu chodziło).

2. a kiedy tak:
liczba także oznacza, {ile kul widać w danym kierunku, ale nie spoza diagramu, tylko z pola zerowego w danym rzędzie}
to liczba ma dwa znaczenia, które muszą być spełnione jednocześnie i do tej wersji ja i @logi wysłaliśmy rozwiązania.
Myślę, że prof. Miodek uznałby obydwie interpretacje za poprawne. 🙂

Rozwiązanie do wersji 1.:
1 0 2 3
3 2 1 0
0 1 3 2
2 3 0 1
Usunięte obie górne dwójki.

Czyli w każdym rzędzie dwóch obserwatorów z jedną liczbą. No może, może… (to a propos protestu).
mp

[kerajs]

Dokładnie jedno rozwiązanie dostaje się usuwając obie dwójki znad diagramu. I jest to jedyna para którą można usunąć zachowując jednoznaczność rozwiązania.