Kwiatek
W ramach rozpoczętej poprzednim wpisem serii łamigłówek, przy których trzeba przysiąść fałdów, zdecydowałem się zaproponować zadanie nadesłane przez „Michała S”. Nawiązuje ono do wpisu „Cc kwadrat” z grudnia ub. roku, a ściślej jest bliźniakiem zamieszczonego tam problemu z kombinatorycznej teorii grup. Znajomość tego działu matematyki nie jest jednak konieczna, aby dotrzeć do rozwiązania, choć nie jest to łatwe.
Tworzymy witraż, który ma być stylizowanym „kwiatem” złożonym z siedmiu sześciokątnych płytek. Dysponujemy płytkami w trzech kolorach.
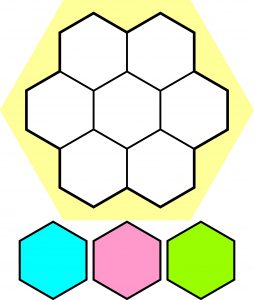
Ile różnych 7-płytkowych (6-płatkowych 🙂 ) kwiatów, czyli wzorów witrażu, można utworzyć w dwu przypadkach:
- gdy dwa wzory uważamy za identyczne, jeżeli w wyniku obrotu jednego powstaje drugi?
- gdy dwa wzory uważamy za identyczne, jeżeli w wyniku obrotu i/lub odbicia lustrzanego jednego powstaje drugi?
Uwzględniamy także możliwość nie skorzystania wcale z jakiegoś koloru, czyli w skrajnym przypadku wszystkie płatki i słupek (słupkowie) mogą mieć ten sam kolor.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Czy warunek: „Uwzględniamy także możliwość nie skorzystania wcale z jakiegoś koloru” oznacza, że płytka może pozostać biała, co w sumie daje cztery kolory?
Nieskorzystanie z koloru oznacza brak koloru, a nie brak płytki. Nie ma białych płytek, są tylko (na początku) miejsca na płytki.
mp
1. 390
2. 276
Próba nr 1:
1. 130
2. 7
W punkcie 2 uwzględniłem dwie symetrie: względem osi pionowej (0 st.) i osi pochylonej o 30 st. (oraz ich obrotów)
Ponieważ nadal nie rozumiem, jak dysponując płytkami w trzech kolorach mógłbym korzystać z tych płytek, ale nie korzystać z ich kolorów, to pomijam ten aspekt.
Odpowiedzi są tak zaskakujące, jakby rozwiązywane było inne zadanie.
Nie rozumiem „nierozumienia”. Skorzystanie z płytki jest równoznaczne ze skorzystaniem z jej koloru.
mp
Ja rozumiem, więc wyjaśnię troszkę wyręczając Gospodarza:
Każde pole musi mieć jakiś kolor (jeden z trzech):
1. morski
2. łososiowy
3. kolor świeżej łąki
Może być CAŁE otwarte morze – czyli siedem płytek „morskich” – wtedy inne/pozostałe kolory nie są wykorzystane.
Efekt synergii – co dwie głowy to nie jedna.
Oho, znowu mój ulubiony lemat Burnside’a.
Same obroty: (2^7+2*2^2+2*2^3+2^4)/6 = 28
Obroty i symetrie: (2^7+2*2^2+2*2^3+2^4+3*2^5+3*2^4)/12 = 26
To jest oczywiście OK, ale dla 2 kolorów.
mp
@mp 194022
„Nieskorzystanie z koloru oznacza brak koloru, a nie brak płytki”
@mp 194024
„Skorzystanie z płytki jest równoznaczne ze skorzystaniem z jej koloru”
Wprawdzie miniony tydzień spowodował, że przemęczenie zabiło u mnie zdolność do logicznego myślenia, ale mimo to uważam, że powyższe dwa zdania są sprzeczne.
Może powinienem 194022 sformułować tak:
„Nieskorzystanie z (danego) koloru oznacza brak (tego) koloru, a nie brak płytki (z jakimś innym kolorem)”.
mp
Próbowałem ręcznie, ale się poddałem…
Komputer pomógł:
1. 390
2. 276
I jeszcze wyniki dla innej liczby dostępnych kolorów:
1: 1/1
2: 28/26
3: 390/276
4: 2800/1720
5: 13175/7525
6: 46956/25746
7: 137788/73696
8: 350400/184416
9: 798525/415665
Próba nr 2
Na razie punkt 1: 390
P.S.
@apartado 194025
@mp 194027
Takie rozumienie jest oczywiste i wynika z treści zadania („dysponujemy płytkami”…). Dlatego dodatkową uwagę w drugim akapicie drugiego przypadku zrozumiałem, jako nowy warunek – płytkę bez właściwości – białą, przeźroczystą, pozbawioną w ogóle cechy koloru. A to tylko redundancja…
Panie Marku,
Koleżanka, które zwykle ma rację w takich kwestiach, twierdzi, że 402 i 312.
Mnie natomiast wyszło 372 i 304, jednak nie ufam swojej wyobraźni w zakresie zliczania liczby permutacji dla poszczególnych przekształceń (obrotów i symetrii)
Dlatego obstawiam: 402 i 312.
W każdym razie – zadanie chodzi nam po głowach od soboty niemal nieprzerwanie, niezależnie od poprawności któregoś z naszych wyników, jest świetne!
Ciepło, ciepło…
mp
390
276
1) 390
2) 276
PS
Obroty i odbicia – lemat Bruce’a Lee w sali luster.
402 i 312 uzyskały komentarz: ciepło, ciepło. Mam cichą nadzieję na: cieplej, cieplej.
Trochę na wariata strzelam dla wariantu 2: 384