Trudniej

21 marca 2020
Marek Penszko

Więcej, częściej, trudniej – takie postulaty pod adresem łamiblogera zgłaszają uwięzione w domach przez koronawirusa znudzone rzesze wytrawnych główkołamaczy. Z tymi „rzeszami” to oczywiście żart. Ot, było kilka sugestii, zatem wypada się odnieść.
A więc: więcej i częściej nie będzie, bo łamiblogowanie to relaks i jedno zadanko raz na tydzień jest częstotliwością i porcją optymalną, aby relaksem pozostało. Natomiast z trudniejszymi problemami nie ma problemu. Ściślej, nie chodzi o podwyższoną matematykę, ale raczej o większą pracochłonność. Zatem dziś będzie ekstremalnie.
Przed miesiącem pisałem o krzyżowaniu kwadratów. Chodzi o układanie miniaturowych krzyżówek liczbowych, w których wszystkie wyrazy-liczby są kwadratami. Zadanie polegało na ułożeniu krzyżówki prostokątnej białej, czyli takiej, której diagram jest prostokątem, nie zawierającym ani czarnych pól, ani tzw. przerywników. Uraczyli mnie Państwo wówczas takimi oto trzema dziełkami – 3×2, 5×3 i 7×4:

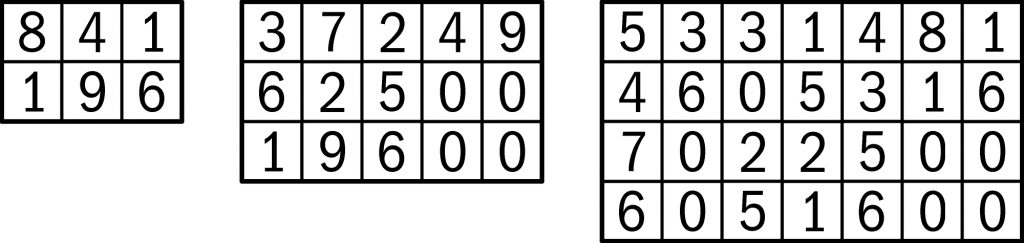
Największe wrażenie robi oczywiście dziełko trzecie. Jednak to nie wszystkie możliwości. Zdziwiło mnie pominięcie przez autora 7×4 („apartado”) mniejszego diagramu, bo nie wątpię, że w szukaniu tej perełki uczestniczył komputer. Czyżby nawet maszyna nie była w stanie poradzić sobie ze znalezieniem krzyżówki 5×4 z czterema poziomymi 5-cyfrowymi i pięcioma pionowymi 4-cyfrowymi kwadratami? Próbowałem szukać na piechotę i wydaje mi się, że jest to zadanie na godzinę intensywnego, ale oczywiście wspartego logiką dłubania lub na kilka dni na raty. Na napisanie programu też trzeba przeznaczyć około godziny, choć tu mogę się mylić, bo programowanie nie jest moją mocną stroną. A zatem kto ma ochotę i cierpliwość – do dzieła. Dla zachęty przykład, ale wybrakowany, bo tylko z ośmioma kwadratami – nie jest nim jedna liczba (która?).

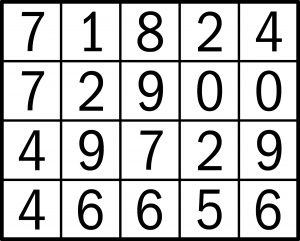
I jeszcze informacja, która może być ułatwieniem: w szukanej krzyżówce występuje każda z cyfr od zera do dziewięciu (w powyższym ułomnym przykładzie brakuje trójki).

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.