Same kwadraty
Liczbomani(acy) i autorzy zadań bawią się czasem w krzyżowanie kwadratów, czyli układanie miniaturowych krzyżówek liczbowych, w których wszystkie „wyrazy” są kwadratami. Ideałem jest, aby krzyżówka była pełnym prostokątem, no i oczywiście aby liczby były różne. Teoretycznie najmniejszą prostokątną krzyżówkę stanowi diagram 2×1 z poziomym kwadratem 49 oraz jednocyfrowymi pionowymi – 4 i 9:
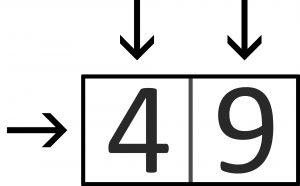
Liczbowe dwa wymiary zaczynają się jednak od diagramu 2×2, ale ulokować w nim kwadratów nie sposób, bo nie ma dwu różnych dwucyfrowych kwadratów zaczynających się taką samą cyfrą.
Czy znajdą się różne kwadraty, którymi będzie można wypełnić większe prostokątne diagramy, od 3×2 poczynając? Zostawiam państwa z tym pytaniem, uzupełniając je nieprostokątną krzyżówką do wypełnienia dziewięcioma wyrazami-kwadratami – czterema poziomymi i pięcioma pionowymi, w tym jednym 4- i jednym 5-cyfrowym.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.)

Komentarze
Rozwiązanie zadania uzupełniającego (jedyne):
http://pokazywarka.pl/kwadratyu/
Znalazłem prostokąt 3×2 (jedyny):
8 4 1
1 9 6
znaczy „znajdą się”.
Czy i jak można to ustalić dla dowolnych rozmiarów prostokąta, na razie nie wiem – jestem bardzo zajęty rozwiązywaniem problemu Flawiusza 🙂
Prostokątów 3×3 jest od groma, ale to dlatego, że są symetryczne. Tu jedynie trzy przykładowe:
1 2 1
2 5 6
1 6 9
1 6 9
6 7 6
9 6 1
1 4 4
4 0 0
4 0 0
Ciekawe, czy można ugryźć to teoretycznie dla dowolnego prostokąta?
Mnie, jak już pisałem, pochłonął całkowicie problem Flawiusza – jest nie z tej Ziemi, fascynujący. Rozwiązałem go dla k=5 i pracuję dalej. Szkoda, że akurat za to nikt nie oferuje 1M$ nagrody…
Chodzi o prostokąty z RÓŻNYMI kwadratami.
A w przypadku Flawiusza wydaje mi się, że odkrywana jest Ameryka – choć to oczywiście też przyjemne.
mp
3×2 można wypełnić liczbami:
841
196
Diagram podany wyżej to:
_ _ 1 6
_ _ 5 7 6
4 3 2 6 4
9 6 1
Prostokąt 3×2: 841/196
Diagram – liczby poziome: 16, 576, 43264, 961
__16
__576
43264
961
Wraz z rosnącą ilością cyfr, kwadratów jest coraz więcej, wydaje się więc, że wypełnianie prostokątów tymiż, powinno być coraz łatwiejsze 😉
37249
62500
19600
Wydaje się… ale liczba końcówek kwadratów jest ograniczona.
mp
Prostokąt 3×2
841
196
Wielobok
__16_
__576
43264
961__
3×2 się da:
841
196
zagadka główna:
1 6
5 7 6
4 3 2 6 4
9 6 1
Pozdrawiam
W nieprostokątnej krzyżówce znajdą się kwadraty następujących liczb:
Poziomo od góry: 4, 24, 208, 31
Pionowo od lewej: 7, 6, 39, 26, 8.
Sprawdzałem kolejne możliwości dla liczby trzycyfrowej czwartej poziomo od góry i dopiero ostatnia możliwa, czyli 961, przyniosła sukces.
Żeby trochę poszerzyć horyzont zdarzeń:
5331481
4605316
7022500
6051600
Super!
mp
@Gospodarz
„A w przypadku Flawiusza wydaje mi się, że odkrywana jest Ameryka”
Jestem zadziwiony tą opinią. Ameryka jest od dawna odkryta, a problem Flawiusza to nadal terra incognita. Brak paraleli.
Zgłębianie zagadki i jej zrozumienie to coś innego, niż przeczytanie w Wikipedii, że wybitni matematycy jeszcze nie znaleźli rozwiązania. To w 99,99% przypadków podążanie po śladach, ale zawsze istnieje ten 0,01% nieznanego terytorium, będącego nadzieją na odkrycie.
P.S. Na marginesie, właśnie w taki, bardzo przekorny sposób, odkryłem niezwykły wzór na unię dwóch ciągów arytmetycznych. Wzór z podstaw teorii liczb, a jednak dotychczas nieznany. Prosta rzecz, a jednak zajęło mi to kilka lat!
https://vixra.org/author/waldemar_zielinski
Udowodniłem też (jeszcze nieopublikowane, wymaga czasu), że nie istnieje wzór na unię trzech(!) i więcej ciągów arytmetycznych, a w konsekwencji – jaka szkoda – że nie istnieje wzór na n-tą liczbę pierwszą. Przynajmniej w ortodoksyjnej teorii liczb. A to już nie są żarty.
Matematyka nie jest ograniczoną barierami dziedziną nauki. To, że przez kilkaset lat nikt nie znalazł rozwiązania, nie oznacza, że rozwiązanie nie istnieje. Trzeba to jeszcze udowodnić. Póki takiego dowodu nie ma, a głowili się nad nim mocarze, proszę nie pozbawiać nadziei nielicznych walczących.
300: Początek imperium
δόξα στους ήρωες
Napisałem „wydaje mi się”, bo temat jest tak mocno przewałkowany, że znalezienie czegoś nowego graniczy z cudem. Ale cuda się zdarzają, więc życzę powodzenia. Przy okazji: w pakiecie kombinatorycznym Wolframa jest funkcja, która z problemem Flawiusza radzi sobie migiem:
https://reference.wolfram.com/language/Combinatorica/ref/Josephus.html
mp
PS stwierdzenie „udowodniłem” nie oznacza „zostało udowodnione”.