Cc kwadrat
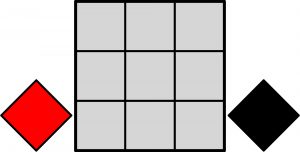
W każdym z 9 pól szarego kwadratu 3×3 należy umieścić, jak w witrażu, czerwoną lub czarną szklaną płytkę. Ile różnych czerwono-czarnych wzorów uda się w ten sposób utworzyć w kwadracie w dwu przypadkach:
- gdy dwa wzory uważamy za identyczne, jeżeli w wyniku obrotu jednego powstaje drugi?
- gdy dwa wzory uważamy za identyczne, jeżeli w wyniku obrotu i/lub odbicia lustrzanego jednego powstaje drugi?

Komentarze
Czarne=0, czerwone=1, puste centralne pola to 0 lub 1.
Rysuję tylko układy dla liczby jedynek mniejszej lub równej 4. Pozostałe uzyskuje się zamieniając wszędzie jedynki z zerami.
1. Obroty
—
Unikalne układy z bez obrotu są dwa:
000
0 0
000
010
1 1
010
Po zamianie 0 z 1 będzie 4.
Puste miejsca to 0 lub 1 więc razem 8.
u1=8
—-
Układy z jednym obrotem o 90 stopni są trzy:
010
0 0
010
100
0 0
001
110
0 0
011
Puste miejsca to 0 lub 1 więc razem 6.
Po zamianie 0 z 1 będzie 12.
Po obrocie o 90 stopni mamy u2=24
Unikalnych, bez obrotu, jest więc:
u2’=u2/2=12
—-
Wszystkich układów jest 8^3=512.
Układów z trzema obrotami jest:
u3=512-u1-u2=512-8-24=480
Unikalnych jest więc:
u3’=480/4=120
Wszystkich unikalnych wzorów „odpornych” na obroty jest razem:
u=u1+u2’+u3’=8+12+120=140
—
Drugą wersję, z odbiciami, to już chyba innym razem. Dał pan, Gospodarzu, do pieca – czacha mi aż dymi…
—-
1) 136
2) 90
Mam kłopot z analitycznym rozwiązaniem pkt 2. Trzy metody i trzy różne rezultaty. Skleciłem więc program, który dał mi zaskakujący wynik: 126. Dobry?
Niedobry, ale to jest istotnie bardzo trudne – raczej matematyczne niż łamigłówkowe (macierze, teoria grup). Chyba przegiąłem.
mp
Niewykluczone, że wygooglowane przeze mnie wartości są tymi, które zaspokajają warunki zadania.
1. 160
2. 102
Googlowanie połowicznie efektywne.
mp
A tak na szybkiego, bez zastanowienia:
2^9=512
obroty: 512/4=128
z odbiciami: 128/2=64 ?
chyba nie, skoro wspomniano o macierzach i teorii grup 🙁
W pierwszym przypadku wyszło mi 140:
– cały witraż czarny, cały witraż czerwony – 2 sztuki
– jedna szybka inna od reszty szybek – 6 sztuk
– dwie szybki inne od reszty szybek – 20 sztuk
– trzy szybki inne od reszty szybek – 44 sztuki
– cztery szybki inne od reszty szybek – 68 sztuk
Proszę o odpowiedź, czy to dobry wynik.
W wygooglowanym materiale doczytałem, że jednak nie 160 a 140, więc ostatecznie obstawiam tak:
1. 140
2. 102
2. Odbicia (kontynuacja)
Czarne=0, czerwone=1, puste centralne pola to 0 lub 1.
Rysuję tylko układy dla liczby jedynek mniejszej lub równej 4. Pozostałe uzyskuje się zamieniając wszędzie jedynki z zerami.
Na początek spostrzeżenie: jeśli układ ma oś symetrii pionową, poziomą, prawoskośną lub lewoskośną to wśród rozwiązań z zadania 1 nie ma on odbicia lustrzanego, gdyż albo sam jest swoim odbiciem, albo jego obrót. Wyjątkiem (chyba?) są układy nie mające osi symetrii, ale mające środek symetrii, gdyż mają jednak odbicie lustrzane nieusunięte w zadaniu 1.
Szukamy więc układów niesymetrycznych osiowo. Takie układy nie mogą mieć jednej jedynki (jednego zera) gdyż są równoważne ze swoim obrotem.
Pozostają układy z 2 i 3, 4 jedynkami poza środkiem. Te z 5, 6 i 7 jedynkami uzyskuje się z układów z 2, 3 i 4 zerami po zamianie kolorów.
—
Niesymetryczne układy z dwiema jedynkami poza środkiem są 2:
110 | 100
0_0 | 0_1
000 | 000
Wszystkie pozostałe „dwujedynkowce” są albo ich obrotami, albo odbiciami. W środku może być 0 lub 1, więc razem 4 układy. Po zamianie kolorów razem: 8.
—
Niesymetrycznych układów z trzema jedynkami jest 4:
110 | 110 | 110 | 110
0_1 | 0_0 | 0_0 | 0_0
000 | 001 | 010 | 100
Więc wszystkich jest 16.
—
Niesymetrycznych układów z czterema jedynkami jest 7:
111 | 111 | 111 | 110 | 110 | 110 | 110
0_1 | 0_0 | 0_0 | 0_1 | 0_1 | 1_1 | 0_0
000 | 001 | 100 | 010 | 100 | 000 | 101
Tutaj zamiana kolorów nic nie daje (cztery jedynki i cztery zera), więc uwzględniając tylko 0 lub 1 w środku mamy 14.
—
Razem układów mających odbicia wśród wyników z zadania 1 jest: 8+16+14=38
Układów spełniających warunki zadania 2 jest: 140-38=102. Howgh!
P.S. @mp: „Chyba przegiąłem”.
Szanowny panie Marku! Wręcz przeciwnie. Przegięciem są zadania, które rozwiązuje się w 6 minut, czasem w 16, co widać po godzinach ich nadesłania. To jest pierwsze zadanie od bardzo dawna, które wymaga rzeczywistego pogłówkowania. Nikt na tym nie ucierpi. Nawet jeśli ja, czy ktoś inny nie znajdzie rozwiązania, to sam fakt spędzenia paru godzin nad czymś ambitniejszym jest bezcenny.
Dziękuję za to zadanie i zachęcam do publikowania podobnych od czasu do czasu (byle nie za rzadko).
W drugim przypadku wyszło mi 102:
– cały witraż czarny, cały witraż czerwony – 2 sztuki
– jedna szybka inna od reszty szybek – 6 sztuk
– dwie szybki inne od reszty szybek – 16 sztuk
– trzy szybki inne od reszty szybek – 32 sztuki
– cztery szybki inne od reszty szybek – 46 sztuk
Oba wyniki (ten i z poprzedniego komentarza) – poprawne
mp
O, to świetnie, że poprawne. Obeszło się bez macierzy i teorii grup (cokolwiek to jest). Oznaczyłam poszczególne szybki literami od A do I, następnie kalkulatorem do permutacji otrzymałam wszystkie zestawy 2-, 3- i 4- literowe. Napisałam 8 makr w Wordzie, siedem typu „znajdź i zamień” jedne litery na inne i jedno w celu odrzucenia powtarzających się zestawów.
Można szybko zauważyć, że liczby będą parzyste (bo układów z x czerwonymi jest tyle samo co z x czarnymi). Wystarczy policzyć układy z 0,1,2,3,4 czerwonymi i pomnozyć przez 2.
1) 140
2) 102
rozwiązane komputerowo po tym jak zacząłem się gubić przy 3 czerwonych i odbiciach z obrotami.
Pozdrawiam,
1) 138
2) 102
(1) prawie dobrze. (2) całkiem dobrze.
mp
https://oeis.org/A047937
https://oeis.org/A054247
A liczy się to, korzystając z lematu Burnside’a https://en.wikipedia.org/wiki/Burnside%27s_lemma
liczba istotnie różnych wzorów = średnia (po wszystkich elementach grupy przekształceń utożsamiających nasze wzory) z liczby wzorów zachowywanych (czyli przeprowadzanych same na siebie) przez dane przekształcenie.
U nas:
identyczność: zachowuje wszystkie 2^9 wzorów
obrót o 90 stopni: 2^3 (jeśli ustalimy kolor środka, jednego narożnika i jednego pola krawędziowego, to reszta ma ustalone kolory)
obrót o 180 stopni: 2^5
symetria względem osi równoległej do boku: 2^6
symetria względem przekątnej: też 2^6.
Podstawiamy i mamy:
dla samych obrotów 1/4 * (2^9+2*2^3+2^5) = 140
dla obrotów i symetrii: 1/8 * (2^9+2*2^3+2^5+4*2^6) = 102
A dla 4×4 rozwiązaniem pierwszego wariantu jest 16456. Sam tego nie sprawdzałem, ale to wynika z ciągu A047937 w OEIS
Zamiast lematu Burnside’a można zastosować twierdzenie Polya. Rozwiązanie jest oczywiście bardzo podobne, ale moim zdaniem bardziej czytelne.
W pierwszym przypadku mamy grupę czterech obrotów: o 0 stopni, 90, 180 i 270. (Można to potraktować jako obrót o 90 stopni do potęgi kolejno 0, 1, 2 i 3.)
Jeżeli ponumerujemy kwadraty w następujący sposób:
123
456
789
to dla poszczególnych obrotów mamy permutacje:
– 0 stopni: (1)(2)(3)(4)(5)(6)(7)(8)(9) – razem 9 permutacji
– 90 stopni: (5)(1397)(2684) – razem 3 permutacje
– 180 stopni: (5)(19)(28)(37)(46) – razem 5 permutacji
– 270 stopni: (5)(1793)(2486) – razem 3 permutacje
Ponieważ mamy do dyspozycji 2 kolory, będziemy podnosić 2 do potęgi równej liczbie permutacji. Tak więc średni indeks cykli:
P = (2^9+2^3+2^5+2^3)/4= (512+8+32+8)/4=140
Symetria względem osi poziomej daje 6 permutacji: (4)(5)(6)(17)(28)(39). Po 6 permutacji dają też symetrie względem osi pionowej i obu przekątnych. Dla tego przypadku średni indeks cykli:
P=(2^9+2^3+2^5+2^3+4*2^6)/8=(512+8+32+8+256)/8=102