Ślepe zaułki

30 listopada 2019
Marek Penszko

Japońscy główkołamacze od kilku lat intensywnie lansują nieco zakręconą łamigłówkę w „malowanie labiryntu”, która debiutowała w kwartalniku Nikoli 1/2014. Nie wydaje mi się zbyt kusząca, ani zbyt oryginalna (przypomina nurikabe), ale ma swój pokrętny urok, więc zasługuje na gościnę w Łamiblogu.

Diagram podzielony jest na działki. Niektóre z nich należy zaczernić tak, aby te, które pozostaną białe, tworzyły spójny obszar w postaci korytarza o szerokości jednej kratki. Korytarz może, a nawet powinien mieć odnogi, czyli „ślepe zaułki”, ale nigdzie nie może tworzyć pętli. Nigdzie też nie może pozostać ani pojawić się biały lub czarny kwadrat złożony z 4 kratek (2×2). Białe muszą pozostać działki z literami, kółkami i trójkątami. Droga biegnąca białym korytarzem od S do G powinna przechodzić przez wszystkie kratki z kółkami, ale nie może zaliczać żadnej kratki z trójkątem. Inaczej mówiąc, trójkąty muszą być w ślepych zaułkach (nie znaczy to jednak, że nie może być zaułków bez trójkąta).
Przykład

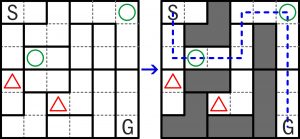
Zadanie

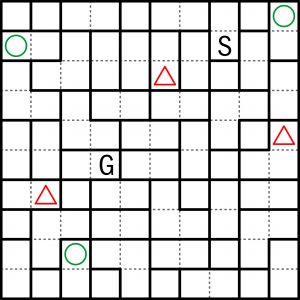
W rozwiązaniu można podać liczbę zakrętów na drodze od S do G (w przykładzie są tylko 4 ).