Inna podstawa

4 lipca 2019
Marek Penszko

Jak wie mój 4-letni wnuczek, 3+4=7, czyli

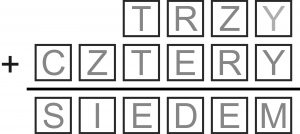
I mamy kryptarytm, zwany też alfametykiem, a więc zadanie, które polega na zastąpieniu liter cyframi tak, aby powstałe w miejsce słów liczby tworzyły poprawne działanie. Łamigłówka wygląda na idealną, bo dodawanie ma sens oraz różnych liter jest dziesięć, czyli dokładnie tyle, co cyfr, a ponadto od razu widać, że układ liter sprzyja rozwiązywaniu na logikę. Do pełni szczęścia przydałoby się jeszcze jedno i tylko jedno rozwiązanie. Niestety, elegancka logika dość szybko prowadzi na manowce, bowiem okazuje się, że rozwiązania brak: cztery cyfry, które pozostają po przyporządkowaniu sześciu pozostałych literom DEIRTZ w żadnym przypadku nie pasują do równań C+1=S oraz 2Y=M (lub M+10).
Sposób na „uratowanie” zadania jest jeden: przenieść się do innego systemu liczbowego – oczywiście takiego, którego podstawa jest większa niż 10. Tym samym alfametyk oddali się nieco od ideału, bo liter będzie mniej niż cyfr. Ale trudno – nic za darmo.
Ponieważ mocno tkwię w systemie dziesiętnym i bardzo niechętnie go opuszczam, więc wiem z doświadczenia, że w pierwszej chwili po takich przenosinach się „głupieje”. Nowicjusz, który ma coś rozwiązać w systemie innym niż dziesiętny z reguły po prostu nie wie, jak to ugryźć. Zwykle jednak krótkie samokształcenie i odrobina praktyki pozwala przełamać opór materii. Dlatego ośmielam się zaproponować chętnym śmiałkom rozwiązanie powyższego alfametyku w systemie… jedenastkowym. Czy rozwiązanie będzie jedno, czy więcej – to także zagadka.