Fuzuli 100

4 kwietnia 2019
Marek Penszko

„Dziękuję za katorżnicze zadanie; masochiści i komputery będą w siódmym niebie” – tak odpowiedziałem na propozycję twardego orzecha do Łamibloga, nadesłaną przez kolegę główkołamacza, którego zadania już tu kilkakrotnie gościły i zawsze były dziełkami z górnej półki, także jeśli chodzi o stopień trudności. Tym razem doszedłem do wniosku, że granice ekstremalnego sportu umysłowego zostały przekroczone. Ponieważ jednak nie wykluczam, że to ja jestem za cienki albo po prostu czegoś nie dostrzegam, więc zdecydowałem się podrzucić tego ładnego „widokowo” orzecha zaglądającym tu wiewiórkom w nadziei, że którejś uda się go rozgryźć bez wspomagania się elektroniką.
Rodzaj zadania zapewne niektórym z Państwa jest znany. Fuzuli ma turecki rodowód i w zamierzchłych czasach gościło w Łamiblogu, a ostatnio pojawiło się na Mistrzostwach Polski w Łamigłówkach. Diagram fuzuli dotąd nigdy nie bywał większy niż 8×8, co zdopingowało kolegę do przekroczenia tych wymiarów.
Zasady zabawy są pomysłową i formalnie prostą wariacją na temat kwadratu łacińskiego.
Do niektórych pól kwadratowego diagramu n×n należy wpisać cyfry od 1 do N (N<n) tak, aby:
– w każdym wierszu i w każdej kolumnie znalazło się N różnych cyfr;
– żadne cztery kratki, tworzące kwadrat 2×2, nie były wypełnione cyframi.
W przykładzie (5×5) N=3

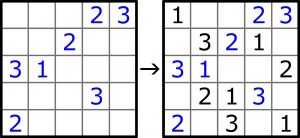
W zadaniu (10×10) N=7

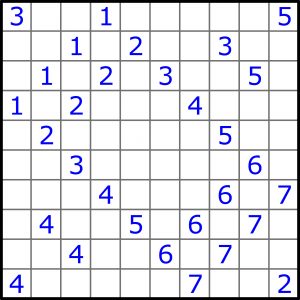
W rozwiązaniu wystarczy podać dziesięć cyfr w polach na przekątnej, łączącej lewy górny róg z prawym dolnym (zera w pustych polach).
Co ciekawe: po usunięciu sześciu cyfr z obszarów narożnych [3, 2, 3-5, 4-4] rozwiązanie także jest jedno.