Zgryz
Jak poprzednia łamigłówka była dość łatwa, tak poniższa jest nietypowym i twardym orzechem dla wybrańców. Niby takie zagadki, zwane indukcyjnymi, goszczą od czasu do czasu w Łamiblogu, ale tym razem okoliczności są szczególne.
Od tygodnia gapię się, a raczej pogapuję jak sroka w gnat na zadanie, które wygrzebałem w starych szpargałach. Pochodzi z jakiegoś japońskiego turnieju dla główkołamaczy z przełomu wieków. Dał mi je przed blisko 20 laty Tetsuya Nishio, z którym miałem wówczas bliski kontakt. Może nawet kiedyś wiedziałem, o co w tym chodzi, ale teraz jestem bezradny. Kombinuję na różne sposoby i nic. Mam oczywiście rozwiązanie i opis – krótki, dwupunktowy, ale japoński, w dodatku pełen znaków kanji, z którymi niełatwo sobie poradzić. Diagram wygląda nawet dość swojsko – poniżej zadanie plus rozwiązanie:
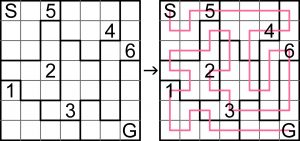
Czy komuś uda się rozszyfrować instrukcję obsługi? Chodzi oczywiście o drugi punkt, bo pierwszy jaki jest, każdy widzi: linia łamana powinna biec od S (sutāto, czyli start) do G (gōru, czyli cel, meta) przez wszystkie pola – przez każde tylko raz.

Komentarze
Rysując linię od Startu i przechodząc przez dana liczbę, musi ona wskazywać liczbę kratek już odwiedzonych w danym obszarze (licząc kratkę z liczbą).
Odpowiem enigmatycznie:
Zgodnie z drugim punktem instrukcji obsługi, pole końcowe (G) ma wartość 7.
Uwolniłem zawczasu bo odpowiedź jest enigmatyczna, a nie błędna, choć może stanowić podpowiedź.
mp
Pole z cyfrą n musi być n-tym polem, przez które przejdzie linia w obrębie obszaru zawierającego cyfrę n.
2. Każda cyfra jest równa liczbie kratek w jej obszarze, które są zajęte przez tę część (różowej) linii, która łączy tę cyfrę ze startem.
@apartado
Udzielając swojej odpowiedzi miałem ochotę napisać co mogłoby być w E1, gdyż wszystkie pozostałe cyfry są przy krawędzi, przez którą przechodzi linia, a pole G takie nie jest. To by chyba nie była oczywista podpowiedź.
Z drugiej strony, z twoją podpowiedzią, suma przekątnych jest równa średniej z liczb! Jak pisałem wcześniej – rzadkie i mocno podniosłoby średnią. Niestety, w diagramie tej siódemki nie ma, więc znowu zaniża średnią. Ot taka dygresja o dziwności Wszechświata…
Punkt 2: Pole z liczbą n ma być n-tym polem obszaru, na którym się znajduje, przez które się przechodzi. Można przy tym oczywiście wychodzić z tego obszaru i wracać, tak jak w przypadku obszaru z liczbą 4. Co ciekawe, rozwiązanie wymyśliło się nie w wyniku intensywnego „wgapiania się”, a po porannym przebudzeniu, gdy przypomniało się zadanie, i pojawił pomysł, że może by tak.
Z cyklu „rozważania wariantowe”:
A gdybyśmy w diagramie łamigłówki zamienili dwójkę na siódemkę, to jaką wtedy wartość miałoby pole G ?
Ależ emocjonujące wprowadzenie do tematu! Jeszcze ktoś gotów uwierzyć, że pan Marek nie wie o co chodzi w tym zadaniu…
Widać że linia łamana rozwiązania wchodzi w pewne relacje z zaznaczonymi siedmioma obszarami, które oznaczę literami A,B,C…G – w kolejności ich „infekowania” przez łamaną. Linia w kolejnych etapach wchodzi do danego obszaru i z niego wychodzi co można zapisać (gubiąc cześć informacji) np. tak:
X m–n (może wstawić inny znak zamiast „–”)
gdzie X – obszar przecinany w danym etapie;
m – „numer infekcji” pola wejścia w danym etapie;
n – „numer infekcji” pola wyjścia w danym etapie;
a „numer infekcji” opisuje, które to jest z kolei infekowane pole tego obszaru.
Jeśli więc łamana infekuje obszar X (wchodzi do niego po raz pierwszy) i wychodzi po zainfekowaniu n pól, to etap ten zapiszemy następująco:
X 1–n
Jeśli po odwiedzeniu innego obszaru łamana wraca do X, infekując kolejne k pól, to taki etap zapiszemy tak:
X (n+1)–(n+k)
Oto zapis wszystkich etapów podanego rozwiązania:
A 1–5 ..–5
B 1–3
C 1–2
B 4–6 4–..
D 1–2
C 3–6 ..–6
E 1–3
C 7–7
E 4–4
D 3–4 3–..
F 1–2 ..–2
D 5–6
B 7–7
F 3–4
A 6–7
F 5–7
G 1–5 1–..
D 7–7
G 6–7
E 5–7
Warunki zadania ujawniają część informacji o przebiegu rozwiązania, pokazaną powyżej po prawej stronie. Są to „numery infekcji” na przemian pól wyjścia i wejścia (ale czasem pierwszego, a czasem drugiego). Dla obszaru E nie ujawniono żadnej informacji.
_____________________________________
Jeden problem to zauważyć te relacje, drugi, nie mniejszy, czytelnie je opisać.
Ale chyba najtrudniej byłoby rozwiązać to zadania w normalnym trybie.
@apartado
Bardzo ładne.
Podejrzewam, że uzyskałeś inne rozwiązanie niż 7, gdyż nie byłoby tego pytania. A może byłoby? Diabli wiedzą…
Mnie jednak ponownie wyszło 7, o tak:
http://pokazywarka.pl/japan7/
@xswedc
Zgadza się – ponownie wychodzi 7 na końcu.
Pole końcowe nie może zmieniać swojej wartości 😉
Jest jeszcze drugie rozwiązanie, które odrobinę inaczej prowadzi linię między 1 a 3.
Wchodzi ona do 3 od prawej strony, zamiast od dołu – to wpływa na skrócenie zawijasa końcowego.
Diagram jest podzielony na kafelki (7-elementowe).
Ujawnione w diagramie liczby określają, jako które z kolei w obrębie kafelka mają być odwiedzone przez linię łamaną pola je zawierające.
Lepiej to przeformułować w stylu twierdzenia:
Dla każdej ujawnionej w diagramie liczby n, pole ją zawierające ma być odwiedzone przez linię łamaną jako n-te z kolei w obrębie kafelka.
Nie wiem, czy ktoś tu jeszcze zajrzy, ale dodam, że autorem tej łamigłówki jest Naoki Inaba. I załączam link na jego stronę:
http://inabapuzzle.com/honkaku/route.pdf