Sumy różnic
Na Święta pozostaniemy w Japonii, czyli zapoznamy się z jeszcze jedną łamigłówką, która ma dalekowschodni rodowód. Jest przy tym kontrowersyjna i w zasadzie należy już do przeszłości. Debiutowała bowiem przed blisko dekadą i… nie przyjęła się. Należy do zadań opartych na ciekawym i oryginalnym pomyśle, nie owocującym jednak atrakcyjnym „towarem”, na który jest popyt. Rozwiązywanie okazuje się po prostu zbyt zakręcone lub raczej zaplątane, co związane jest z kluczowym dla tego pomysłu sprzężeniem zwrotnym.
Zasady są proste, choć niełatwo zwięźle je przedstawić. W puste pola należy wpisać liczby naturalne dodatnie. Wszystkie one, także te, które są już wpisane, powinny spełniać pewien warunek. Aby go przedstawić pozwolę sobie na pewną rozwlekłość.
Każda liczba X sąsiaduje przynajmniej z jedną, a co najwyżej z czterema innymi liczbami. Między liczbą X a każdą z jej sąsiadek występuje jakaś różnica – umawiamy się, że różnica ta jest zawsze liczbą nieujemną. Otóż liczba X, a więc każda liczba w diagramie, powinna być równa sumie tych różnic – jednej, dwóch, trzech lub czterech – między nią a sąsiadkami.
Mam nadzieję, że zasada jest zrozumiała; na wszelki wypadek mały przykład z rozwiązaniem.
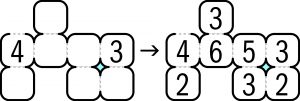
A poniżej zadanie świąteczne.
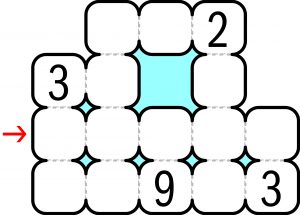
Obawiam się, że (za)danie nie jest zbyt „lekkostrawne”, choć może niektórym Łamiblogowiczom zasmakuje. W rozwiązaniu wystarczy podać ciąg pięciu liczb wskazany czerwoną strzałką.
Spokojnych Świąt.

Komentarze
35563 Fajne!
Wesołych Świąt i Szczęśliwego Nowego Roku! 🙂
35563
35563
W pełni zgadzam się ze słowami Gospodarza w kwestii atrakcyjności „towaru”: na jeden raz to mi smakowało – ciekawość została zaspokojona, ale nie kusi żeby się pochylić nad kolejnym zadaniem z tego gatunku.
Nie będę rozwijał zagadnienia „Gusta Publiczności, czyli co nam smakuje i dlaczego?” – musiałbym nawiązać do kopernikańskiej teorii pieniądza, a to nie czas i miejsce 😉
35563
35563
Zaczynając od 2 mamy sześć kombinacji sąsiednich pól do sprawdzenia:
11, 33, 42, 24, 13, 31
Posuwam się w lewo, w kierunku 3, a tam kolejnych 10 kombinacji:
12, 21, 25, 52, 36, 63, 41, 14, 45, 54
Po znalezieniu tej właściwej, która nie psuje wcześniej wpisanych liczb i umożliwia kontynuację, reszta diagramu idzie już z automatu.
Cały diagram:
X422X
36X4X
35563
47963
Proszę o jeszcze jedno takie haiku.
Ciąg za strzałką to: 3,5,5,6,3.
Moim zdaniem to zadanie pasuje do typu zadań, który dość często gości w
Łamiblogu, a przypomina rozwiązywanie równań różniczkowych cząstkowych w wariancie dyskretnym.
Szukamy bowiem takiej funkcji dyskretnej określonej na wycinku
płaszczyzny/szachownicy, której wartość w każdym punkcie/komórce
spełnia zadane warunki zgodności z wartościami w sąsiednich komórkach.
Brak masowej popularności tego typu zadań nie wyklucza popularności elitarnej,
bo to ciekawy typ zadań i chyba zasługuje na popularyzację.
Ja odczuwam zwykle pewien niedosyt, bo oprócz rozwiązania konkretnego zadania chciałoby się sformułować jakąś metodę czy taktykę rozwiązywania.
Zwykle jednak zaraz pojawia się nowe zadanie i przyciąga uwagę,
a brak już sił i czasu na refleksję czy oprócz rozrywki czegoś nas to nauczyło?
Widzę że coś na kształt metody w zadaniach tego typu to:
1) uchwycić przyczółek, tj. zacząć od jakiegoś punktu,
gdzie łatwo spełnić warunek, tj. znaleźć rozwiązanie lokalnie;
2) opracować odp. miarę odchylenia od spełnienia warunku zadania;
3) wyliczać wartości w sąsiednich komórkach tak, aby zerować miarę odchylenia.
Takie rozwiązywanie przypomina jakby rozchodzenie się epidemii.
W przypadku przykładu wstępnego widać od razu taki przyczółek.
W przypadku zadania trochę trudniej wytypować odpowiedni.
Ale gdy się już znajdzie przyczółek, to rozwiązanie postępuje błyskawicznie.
Tu ilustracja do tych uwag:
https://pokazywarka.pl/lhdwfj/
Wystarczy zauważyć, że na samym początku pomiędzy liczbami 9 oraz 3 musimy wpisać liczbę 6 i potem rozwiązujemy zagadkę (nie jest wcale taka zła) niczym błyskawica otrzymując we wskazanej linijce ciąg 3,5,5,6,3
Pozdrawiam
Radosnych i rodzinnych Świąt Bożego Narodzenia!
Kluczem do rozwiązania tej jednak prostej zagadki jest dolna linia – w szczególności 9 i 3 w rogu. Później już idzie gładko 🙂
Rozwiązanie z zaznaczonej linii: 3, 5, 5, 6, 3.
Dziękuję panie Marku za wspaniałe zadania. To mój pierwszy wpis choć już nie jedną Pana zagadkę rozwiązywałem ale dopiero teraz odważyłem się napisać sprowokowany tym, że „rozwiązywanie okazuje się po prostu zbyt zakręcone lub raczej zaplątane”. Jak widać tak nie jest.
Lubię szczególnie Pana zagadki, które można rozwiązać bez pisania programu.
Dużo zdrowia i równie wspaniałych pomysłów na zadania w nadchodzącym roku!
Dziękuję 🙂
mp
Wszystkiego zdrowego i szczęśliwego, także w następnym 2019 roku.
35563.
Również życzę Wesołych Świąt i wszystkiego co najlepsze w 2019 roku!
Rozwiązanie: 35563
(kluczem było pole pomiędzy 9 i 3 oraz spostrzeżenie, że różnice muszą być też zerowe)
pełne rozwiazanie:
https://app.box.com/s/3qcxczi5y51bu828g2hjfipfkng6qakq
Pozdrawiam,
@xswedc
Haiku?
Bardzo proszę:
Początek zimy
śnieg znowu trochę pada
siedzę przy ogniu
@xswedc
http://pokazywarka.pl/r3b41z/
Reguły są niezmienione poza zamianą liczb na litery:
w puste, białe pola należy wstawić litery z „angielskiego” alfabetu (A-1,B-2, … ,Z-26) tak, żeby każda litera była sumą różnic odległości w alfabecie, czyli żeby była to litera z odpowiedniego miejsca w kolejności alfabetycznej.
Wykorzystam okazję, żeby życzyć wszystkim Lepszego Nowego roku 2019.