Na okrągło
N-cyfrowa liczba kolista jest znamienna tym, że z jej zapisu na kole można odczytać każdą jej wielokrotność od 1 do n, zaczynając za każdym razem od innej cyfry i wykonując jedną rundę zgodnie z kierunkiem zapisu. Gwoli jasności klasyczny przykład, czyli 142857.
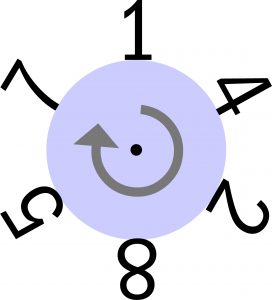
Dwukrotność protoplastki czytamy w kółko, zaczynając od dwójki (285714), trzykrotność – zaczynając od 4 (428571) itd., aż do odósemkowej sześciokrotności, czyli 857142.
Liczbą okrężną nazwiemy krewniaczkę liczby kolistej, różniącą się od niej tym, że odczytywana wielokrotność jest jedna, ale odczytując ją wykonujemy więcej niż jedną, lecz mniej niż dwie rundy (przy dokładnie dwóch okrężną byłaby każda liczba).
O ile wiem, nikt się takimi liczbami jeszcze nie bawił, więc też ich nie szukał. Jednocyfrowe oczywiście wykluczamy, a dwucyfrowa jest chyba tylko jedna – 25 (25×21=525). Kto znajdzie choć jedną trzycyfrową? Dla zachęty czterocyfrowa (jaka?) nawinięta na kółko.
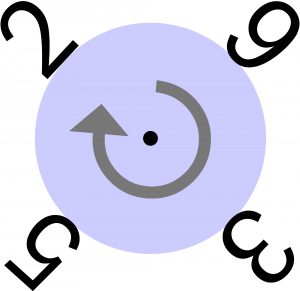
![]()

Komentarze
Komputer znalazł takie liczby okrężne trzycyfrowe:
125 * 41 = 5125
625 * 9 = 5625
625 * 41 = 25625
rozwiązanie czterocyfrowe:
3529 * 15 = 52935
Jako prywatna ciekawostka:
(prywatna – nie do publikacji, bo nie związana w jakiś sposób z bieżącą łamigłówką – taki powiedzmy podarunek mikołajkowy – mam nadzieję, że się spodoba 🙂
Poniższy układ przekształcony według conwayowskich reguł LIFE, pokazuje interesujące następne pokolenie.
„o” to żywa komórka
„.” to komórka nieżywa
Układ jest prostokątny ale formatowanie go zniekształca.
Jest to format przyjmowany jako CTRL+V przez ten program:
http://golly.sourceforge.net/
Po wklejeniu wystarczy nacisnąć spację- to generuje następne pokolenie.
ooo..ooooooo..oo.oo.oo….oooo.ooooo…
o..oo.o..o…..ooo……o..oo..ooo..ooo
o.o.oo.oo.oo…o.o.ooo..o.oo..o..o..oo.
oo..o.o..o.o….o..o..o.o.ooo..ooo..o.o
..o…o..o…o.o.o..o.o..oo……o.oo.o
..o…o..o.ooo.o.o.o….o..o…o.o..o..
…oo.o.oo.ooooo.o.ooo.oo.ooo.o.o.o…o
.o…o.o.o…o..o.o…oo…o.o.o.oo….
.o.oo.o.ooo.oo..oo.o..oooo.o.oo.o.ooo..
Dziękuję. Podoba się, ale nie zaskakuje czymś szczególnym; lub może osobliwości nie dostrzegam.
mp
Czterocyfrowa: 15 x 3529 = 52935
Trzycyfrowe:
125 x 41 = 5125
125 x 201 = 2512
160 x 376 = 60160
250 x 201 = 50250
375 x 201 = 75375
407 x 182 = 74074
625 x 9 = 5625
625 x 41 = 25625
Dzień dobry.
Bardzo proszę o przywrócenie poprzedniego skoczka. Był szlachetny, wysmakowany, dumny. Obiecywał wysoki poziom.
Ten obecny jest jakiś taki estetycznie ułomny i z gęby chyba głupi. Nie lubię go.
Pozdrawiam
Waldemar Zieliński
Przyjrzałem się skoczkowi. Istotnie, nie wygląda zbyt dostojnie. Nie pamiętam jaki był poprzedni, ani kiedy nastąpiła zmiana. Chyba dawno, nawet parę lat temu.
Prośba nie do mnie, ale spróbuję interweniować „u góry”.
mp
„Szczególność” miała polegać na tym, że pojawia się słowo „Łamiblog”- mowa o pierwszym z kolei pokoleniu, które następuje po tym stanie komórek który wysłałem.
Przepraszam jeśli zawracam głowę, ale wydało mi się to ciekawe, bo nieoczywiste do uzyskania.
Jutro sprawdzę dokładniej czy nie popełniłem jakiegoś błędu.
Aaa, super! (wciskałem enter zamiast spacji i leciało hurtem).
Jeśli można, chętnie uwolnię komentarz z Pańskim prezentem, gwoli przypomnienia life’a.
mp
To jest pewnie ten poprzedni:
https://penszko.blog.polityka.pl/wp-content/themes/polityka.1.0/images/headers/micro/penszko.jpg
Chyba trzeba dodać założenie, że liczba nie kończy się na 0, bo (prawie) każda kończąca się na zero byłaby dobra (o ile dopuszczamy wiodące zera w zapisie liczby).
Trzycyfrowe są dwie: 375 i 407, czterocyfrowych 12, pięciocyfrowych 22.
Proszę o przykład (mnożenie) z liczbą kończącą się zerem, która „byłaby dobra”.
mp
3529 x 15 = 52935
625 x 9 = 5625
@Gospodarz
Cieszę się, że się udało.
Oczywiście proszę uwolnić – niech się wszyscy dowiedzą jak Łamibloga kochają 😉
Czterocyfrowa to 3529, 3529×15=52935
Upps, pomyłka – czterocyfrowych jest 13.
A trzycyfrowe tylko dwie? Znam sześć, a nie mam pewności, czy to wszystkie.
mp
Mnożenie jest przez 1; np. 1 * 110 = 0110
Wystarczy wykluczyć zero wiodące, choć mam wątpliwości, czy to konieczne, bo z zerem wiodącym zabawa traci sens – każda liczba jest okrężna (0x * 10 = 0x0).
mp
Ponieważ obiecał Pan próbę ratowania skoczka, więc w zamian uratuję to zadanie:
Trzycyfrowa nie istnieje – po przedłużeniu do czterocyfrowej:
n(100 a3+10 a2+a1)=1000 a3+100 a2+10 a1+a3
Po przekształceniu:
n=a3/(a1+10 a2+100 a3)+10
Lewa strona jest całkowita, a prawa nijak nie chce taka być. Podobnie wychodzi dla przedłużonych do pięciu cyfr. Rozwiązanie jest wprawdzie negatywne, ale jednak rozwiązanie, czyli pozytywne.
Oczywiście w poprzednim „rozwiązaniu” spaliłem debiut rozpoczynając wielokrotność od pierwszej cyfry. Zorientowałem się już w kilka sekund po kliknięciu w ‚opublikuj’ – cóż za refleks! Spróbuję to naprawić:
od drugiej cyfry, wielokrotności 4-cyfrowe: brak
od drugiej cyfry, wielokrotności 5-cyfrowe:
125*201=25125
160*376=60160
250*201=50250
od trzeciej cyfry, wielokrotności 4-cyfrowe:
125*41=5125
od trzeciej cyfry, wielokrotności 5-cyfrowe:
407*182=74074
Po celnej podpowiedzi z liczbą 2-cyfrową (25×21=525) liczba 50250 była podana na tacy, a 25125 leżała tuż pod tacą. Pozostałe, niestety, doniósł majordomus – arkusz kalkulacyjny. Nie widzę, jak w bardziej tradycyjny sposób można by je wyprowadzić.
Poprzedni skoczek był czarny.
Obecny jest jasnobrązowy – czyli biały (bo drewno ma swoje prawa).
Czy zmiana ma związek z wydarzeniami w Pensjonacie „Rybitwa” ?
https://www.google.com/search?q=czarny+ko%C5%84+zabija+noc%C4%85
Gdy otwieram stronę Łamibloga w komórce, to mam szlachetnego czarnego skoczka, a gdy w komputerze – tego z gęby głupiego. Dlaczego? Tej zagadki Łamibloga rozwiązać nie umiem 🙂
Ja też nie. Ale podejrzewam, że czarny jakoś się „utrwalił” w komórce.
mp
Powiedziałem komputerowi: „rób co chcesz, ale żeby mi to nie trwało godzinami”, a on na to:
2 * 11 = 22
2 * 111 = 222
3 * 11 = 33
3 * 111 = 333
4 * 11 = 44
4 * 111 = 444
5 * 11 = 55
5 * 111 = 555
6 * 11 = 66
6 * 111 = 666
7 * 11 = 77
7 * 111 = 777
8 * 11 = 88
8 * 111 = 888
9 * 11 = 99
9 * 111 = 999
10 * 101 = 1010
11 * 101 = 1111
12 * 101 = 1212
13 * 101 = 1313
14 * 101 = 1414
15 * 101 = 1515
16 * 101 = 1616
17 * 101 = 1717
18 * 101 = 1818
19 * 101 = 1919
20 * 101 = 2020
21 * 101 = 2121
22 * 101 = 2222
23 * 101 = 2323
24 * 101 = 2424
25 * 21 = 525
25 * 101 = 2525
26 * 101 = 2626
27 * 101 = 2727
28 * 101 = 2828
29 * 101 = 2929
30 * 101 = 3030
31 * 101 = 3131
32 * 101 = 3232
32 * 726 = 23232
33 * 101 = 3333
34 * 101 = 3434
35 * 101 = 3535
36 * 101 = 3636
37 * 101 = 3737
38 * 101 = 3838
39 * 101 = 3939
40 * 101 = 4040
41 * 101 = 4141
42 * 101 = 4242
43 * 101 = 4343
44 * 101 = 4444
45 * 101 = 4545
46 * 101 = 4646
47 * 101 = 4747
48 * 101 = 4848
49 * 101 = 4949
50 * 101 = 5050
51 * 101 = 5151
52 * 101 = 5252
53 * 101 = 5353
54 * 101 = 5454
55 * 101 = 5555
56 * 101 = 5656
57 * 101 = 5757
58 * 101 = 5858
59 * 101 = 5959
60 * 101 = 6060
61 * 101 = 6161
62 * 101 = 6262
63 * 101 = 6363
64 * 101 = 6464
64 * 726 = 46464
65 * 101 = 6565
66 * 101 = 6666
67 * 101 = 6767
68 * 101 = 6868
69 * 101 = 6969
70 * 101 = 7070
71 * 101 = 7171
72 * 101 = 7272
73 * 101 = 7373
74 * 101 = 7474
75 * 101 = 7575
76 * 101 = 7676
77 * 101 = 7777
78 * 101 = 7878
79 * 101 = 7979
80 * 101 = 8080
81 * 101 = 8181
82 * 101 = 8282
83 * 101 = 8383
84 * 101 = 8484
85 * 101 = 8585
86 * 101 = 8686
87 * 101 = 8787
88 * 101 = 8888
89 * 101 = 8989
90 * 101 = 9090
91 * 101 = 9191
92 * 101 = 9292
93 * 101 = 9393
94 * 101 = 9494
95 * 101 = 9595
96 * 101 = 9696
96 * 726 = 69696
97 * 101 = 9797
98 * 101 = 9898
99 * 101 = 9999
125 * 41 = 5125
125 * 201 = 25125
160 * 376 = 60160
231 * 533 = 123123
250 * 201 = 50250
351 * 385 = 135135
375 * 201 = 75375
407 * 182 = 74074
429 * 686 = 294294
462 * 533 = 246246
481 * 308 = 148148
625 * 9 = 5625
625 * 41 = 25625
693 * 533 = 369369
702 * 385 = 270270
814 * 182 = 148148
819 * 242 = 198198
858 * 686 = 588588
924 * 533 = 492492
962 * 308 = 296296
1126 * 112 = 126112
1250 * 401 = 501250
1280 * 626 = 801280
1875 * 401 = 751875
2381 * 52 = 123812
2454 * 173 = 424542
3125 * 17 = 53125
3125 * 81 = 253125
3125 * 401 = 1253125
3200 * 626 = 2003200
3529 * 15 = 52935
3797 * 21 = 79737
4762 * 52 = 247624
4908 * 173 = 849084
5443 * 8 = 43544
6250 * 81 = 506250
6250 * 401 = 2506250
6400 * 626 = 4006400
9375 * 81 = 759375
9375 * 401 = 3759375
9600 * 626 = 6009600
13649 * 36 = 491364
15625 * 33 = 515625
15625 * 161 = 2515625
15898 * 371 = 5898158
17953 * 443 = 7953179
21964 * 439 = 9642196
24031 * 13 = 312403
28129 * 289 = 8129281
31250 * 161 = 5031250
31250 * 801 = 25031250
35503 * 945 = 33550335
46875 * 161 = 7546875
48062 * 13 = 624806
51359 * 7 = 359513
53524 * 98 = 5245352
62500 * 801 = 50062500
72093 * 13 = 937209
78125 * 33 = 2578125
78125 * 161 = 12578125
85177 * 914 = 77851778
93750 * 801 = 75093750
96124 * 13 = 1249612
Właśnie miałem poprosić o nieujawnianie tego co powyżej- zawiera zbyt wiele liczb niezgodnych z regułami zadania .
Tutaj już poprawiona selekcja:
125 * 41 = 5125
125 * 201 = 25125
160 * 376 = 60160
250 * 201 = 50250
375 * 201 = 75375
407 * 182 = 74074
625 * 9 = 5625
625 * 41 = 25625
625 * 9001 = 5625625
Są to wszystkie trzycyfrowe liczby sprawdzone dla mnożników maksymalnie 4-cyfrowych.
Czyli potwierdza się ilość tych liczb którą podał Gospodarz (6).
My tu gadu gadu…
… a komputer skończył szukanie liczb 4-cyfrowych.
wynik tych poszukiwań:
1126 * 112 = 126112
1250 * 401 = 501250
1250 * 2001 = 2501250
1280 * 626 = 801280
1507 * 4745 = 7150715
1600 * 3751 = 6001600
1606 * 3836 = 6160616
1875 * 401 = 751875
2381 * 52 = 123812
2409 * 3836 = 9240924
2454 * 173 = 424542
2500 * 2001 = 5002500
3125 * 17 = 53125
3125 * 81 = 253125
3125 * 401 = 1253125
3200 * 626 = 2003200
3529 * 15 = 52935
3750 * 2001 = 7503750
3797 * 21 = 79737
4085 * 1324 = 5408540
4762 * 52 = 247624
4908 * 173 = 849084
5387 * 1625 = 8753875
5443 * 8 = 43544
6250 * 81 = 506250
6250 * 401 = 2506250
6400 * 626 = 4006400
9375 * 81 = 759375
9375 * 401 = 3759375
9600 * 626 = 6009600
Niektóre z nich jak widać mają kilka różnych mnożników, ale różnych jest 25.
I tego się będę trzymał 😉
Zagadka:
Czy ktoś skusi się, żeby spróbować oszacować ilość okrężnych liczb pięciocyfrowych?
(To zagadka też dla mnie, bo nie wiem, czy ktoś się skusi).
@apartado
Tak, skusi się! 🙂
Znalazłam 40 liczb 5-cyfrowych okrężnych (więcej niż 1 runda, mniej niż 2). Wszystkie, jak sądzę.
Najczęstszym mnożnikiem jest 4001 – występuje 7 razy. Mnożniki 13 i 6251 występują po 4 razy, a 801 i 20001 po 3 razy.
Najwięcej razy, ale tylko 3, więc co to za rekord, można wymnożyć liczby 15625 (przez 33, 4001 i 36001) oraz 78125 (przez 33, 161 i 10401).
Podam pełną listę, jeśli ktoś sobie życzy, ale może najpierw zadanie 🙂
Znaleźć liczby, które mnoży się tu przez 13. Układają się w ciąg a, 2a, 3a i 4a.
@OlaGM
Naliczyłem ich 41.
A tu (jak się domyślam) mamy rozbieżność:
15625 * 33 = 515625
15625 * 161 = 2515625
15625 * 4001 = 62515625
15625 * 36001 = 562515625
A sednem mojego pytania było OSZACOWANIE, a więc określenie ilości BEZ generowania poszczególnych liczb.
I to pytanie pozostaje otwarte.
OSZACOWANIE:
Proponując powyższe, byłem ciekaw, jakie będzie podejście różnych rozwiązywaczy to tak postawionego zagadnienia.
Moja „wersja wydarzeń”:
Próba oszacowania siły zbioru pięciocyfrowych liczb okrężnych:
Początek ciągu dla x od 1 do 4
0,1,6,25,…
… generuje funkcję,
5/3x^3-8x^2+40/3x-7
… której wynik dla kolejnego x (czyli dla 5) to 68.
Jak widać próba okazała się nieudana – różnica jest spora (ilość liczb dla długości 5 to 41).
Korzystając z okazji życzę wszystkim Spokojnych Świąt