Fort for…
Choć Łamiblog wykluł się i ćwierka pod skrzydłami Polityki, to z natury jest apolityczny. Zdarza mu się jednak sporadycznie o politykę zahaczać, za co bywa z lekka karcony. Mam nadzieję, że tym razem ujdzie mu na sucho.
Prezydent Andrzej Duda zaproponował w trakcie wizyty w Białym Domu utworzenie w Polsce bazy wojsk amerykańskich o nazwie Fort Trump. Wprawdzie do ewentualnej realizacji przedsięwzięcia droga jest droga i daleka, ale znany z wysokiej samooceny prezydent USA zapewne „kupił” ofertę, co stanowiło inspirację do utworzenia następującego kryptarytmu:
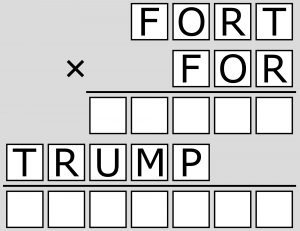
Przypominam instrukcję obsługi.
Pod literami i kratkami w zapisie mnożenia ukrywają się cyfry. Takim samym literom odpowiadają jednakowe cyfry, a różnym – różne. W pustych kratkach mogą pojawić się dowolne cyfry. Należy rozszyfrować działanie, czyli podać wartości czynników i iloczynu.
Zadanie wydaje mi się warte uwagi ze względu na nieco zakręcony i logicznie ciekawy – a przy tym dość prosty – sposób rozwiązywania. Sprawnym główkołamaczom pięć minut powinno wystarczyć.

Komentarze
4061 x 406
lub
7094 x 709
Pani Olu, rozwiązanie jest tylko jedno.
mp
A tak, słusznie, tylko to większe.
7094×709=5029646
7094 × 709 = 5029646
Ale nie zajęło to 5 minut, tylko 15:)
Np. takie działanie spełnia warunki ale nie wychodzą z niego sensowne napisy:
7094 X 709 = (63846 + 49658) = 5029646
czyli
FORT X FOR = (U?PTU + TRUMP) = MO?RUTU
Hmm, o co chodzi w tej zabawie?
Tylko o rozszyfrowanie mnożenia. Nie o szyfrowanie (literami) rozszyfrowanego (liczby w pustych kratkach).
mp
Dopisek, w nawiasie chodziło mi oczywiście o dodawanie pisemne w słupku czyli faktycznie
(63846+49658*100) = 5029646
F^2=TR więc są tylko 4 możliwości, które weryfikujemy przy pomocy F*RT=UMP co daje jedyny wariant 7*94=658.
Ostatecznie mamy: 7094*709=5029646.
7094
x 709
———-
63846
49658
————
5029646
Może zamiast „niesprawnemu”, powiem niewprawnemu główkołamaczowi zajęło to 15 min.
Skoro wyjściowo widzimy, że O = 0 (zero), to dla odkrycia F bierzemy wyłącznie pod uwagę liczby od 4 do 9, a potem sprawdzamy ich potęgi, wykluczając te, które spełniają jeden z poniższych warunków:
1) Ich potęga daje wynik zawierający cyfrę równą potęgowanej liczbie: 5×5=25, 6×6=36.
2) Po mnożeniu potęgowanej liczby przez liczbę uzyskaną wskutek zamiany miejscami cyfr w wyniku potęgowania (TR => RT) powstaje wynik, który zawiera cyfrę będącą już w czynniku: np. 8×8 = 64, 8×46 = 368.
Jedyną liczbą z wybranego zbioru, która nie spełnia żadnego z powyższych warunków jest 7.
Chyba tu chodzi o eleganckie rozwiązanie algebraiczne.
Z postaci działania widać, że O=0 więc działanie to :
(FOR*10+T)* FOR = (1000*F+10*R+T) * (100*F+R)
= (1000*F*R+10*R*R+T*R) + 100*(1000*F*F+10*R*F+T*F)
(konkatenacja symboli to liczba w zapisie pozycyjnym, mnożenie wymaga znaku działania *)
Z postaci działania dostajemy równanie na drugi składnik:
1000*F*F+10*R*F+T*F = 10000*T + 1000*R + 100*U + 10*M + P
skąd
F*F = 10*T+R więc F>3
Możliwe są więc tylko przypadki:
F F*F R T
–––––––––––––––
4 16 6 1
5 25 5 2
6 36 6 3
7 49 9 4
8 64 4 6
9 81 1 8
z których tylko F=7 spełnia warunek:
„Takim samym literom odpowiadają jednakowe cyfry, a różnym – różne.”
7094 x 709 = 5029646
Zajęło więcej niż 5 minut, ale mniej niż 50. O musi być 0, i tak naprawdę chodzi o to, by FORTxF dawało TRUMP, no i FORTxR dawało liczbę pięciocyfrową, o co znacznie łatwiej. Rozwiązaniem jest 7094×7=49658, czyli w pierwszej linijce pod kreską będzie 63846 (=7094×9), a końcowy wynik mnożenia to 5029646 (=7094×709).