Strzałkomino bis
Zagadka indukcyjna z poprzedniego wpisu była bardzo trudna, więc powinienem napisać, że aż jedna osoba (kobert – gratulacje!) ją rozwiązała, czyli rozszyfrowała główną regułę zadania.
Całość instrukcji obsługi strzałkomina brzmi zatem tak:
Na diagramie rozmieszczono pewną liczbę kamieni domina strzałkowego. Każdy zakrywa parę pól, lecz kamienie nigdzie nie stykają się bokami (rogami mogą). Wszystkich różnych kamieni jest sześć – jak na rysunku poniżej (na żadnym strzałka nie wskazuje na strzałkę) – ale wśród ulokowanych na diagramie każdy może występować więcej niż raz lub wcale.
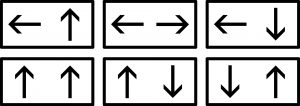
Granice kamieni oraz niektóre strzałki usunięto z diagramu. Mogło być nawet tak, że znikły całe kamienie. Na podstawie pozostawionych fragmentów należy odtworzyć położenie i rodzaje wszystkich kamieni, a podstawowym kluczem do rozwiązania jest następująca informacja:
z trzech możliwych zwrotów każdej strzałki właściwy jest ten, przy którym strzałka wskazuje na najdłuższy ciągły rząd pustych pól.
Gwoli jasności prosty przykład z rozwiązaniem znajduje się w poprzednim wpisie, zaś poniżej propozycja zadania trudniejszego niż poprzednio, ale oczywiście łatwiejszego niż ubiegłotygodniowa zagadka indukcyjna.
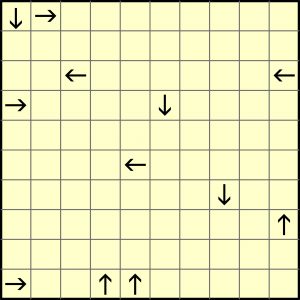
W rozwiązaniu wystarczy podać liczbę strzałek wskazujących w każdym kierunku (N, E, S, W).
PS 14:06 – poprawiony diagram (strzałka w lewym górnym rogu skierowana w dół)

Komentarze
Strzałka w lewym górnym rogu diagramu powinna być skierowana w dół (inne orientacje są sprzeczne z regułami zadania; ewentualnie mogłaby być w lewo, gdyby diagram traktować jako zapętlony).
Dziękuję. Poprawiłem.
mp
„Wszystkich różnych kamieni jest sześć – jak na rysunku poniżej (na żadnym strzałka nie wskazuje na strzałkę) – ale wśród ulokowanych na diagramie każdy może występować więcej niż raz lub wcale.”
Czy to na pewno jest reguła? Wydaje mi się, że w przykładzie do poprzedniego wpisu występowały 3 różne kamienie (pomijając obroty) przy czym Dół-Góra (wg pozycji z rysunku) dokładnie jeden raz (Góra-Prawo 2x, Lewo-Góra 3x).
Istotnie, ale dobór kamieni w przykładzie nie jest sprzeczny z cytowanym fragmentem instrukcji – niektóre kamienie występują co najmniej raz, a inne wcale.
mp
N-6, E-9, S-7, W-6.
7S, 9E, 6N, 6W.
W moim przypadku rozwiązywaniu strzałkomin sprzyja jazda pociągiem.
W moim też – i nie tylko strzałkomin.
mp
N6
E9
W6
S7
Zadanie średnio trudne.
Myślę, że jedną z reguł mogłaby być analogiczna do tej w nurikabe: pola nie pokryte dominami powinny tworzyć spójny obszar.
Dawałoby to możliwość konstruowania bardziej skomplikowanych zagadnień (analiza diagramu obejmowałaby często cały obszar łamigłówki).
Dodatkowo rozważyłbym możliwość użycia formuły „liar”: np. jedna ze strzałek mogłaby wskazywać niewłaściwy kierunek.
Po Łamiblogowym wpisie 24.03.2018 „Kłamigłówka” – lubię tę formę podpowiedzi – w ostatnich dniach miałem bliskie relacje z „liar loops”.
W 3. rzędzie są 2 strzałki o tym samym zwrocie. Czy to oznacza, że te strzałki pokazują 2 osobne ciągi, zaczynające się bezpośrednio przed ich grotami, mające po tyle samo pól?
@OlaGM
Gospodarz tłustym drukiem zaznaczył kluczową regułę.
Zakończyłbym to zdanie słowami: … , który można „zobaczyć” z danego pola w jednym z czterech kierunków N,E,S,W.