Słupki rosną
Sprawdzam na znajomych główkołamaczach stopień trudności zadań szykowanych do kolejnego „Omnibusa”. Wprawdzie z redakcji i spoza niej docierają do mnie najczęściej opinie, że zadania w „Omnibusach” łatwe nie są, ale jednak nie chciałbym przesadzić. Najwięcej wątpliwości mam w przypadku łamigłówek, przy których rozwiązujący mają kłopot z ustaleniem, jak daną rzecz w ogóle ugryźć. Kłopot dotyczy zadań choć trochę nietypowych i jest zwykle stanem przejściowym – kończy się w momencie, gdy rozwiązujący zaczyna zaskakiwać i stopniowo odkrywa ścieżki wiodące do celu. Jeśli jednak wpadnięcie na właściwy trop trwa zbyt długo, zaczynam mieć wątpliwości, czy nie przeginam. Taka sytuacja wiąże się z poniższym rodzajem zadania.
Diagram pokratkowany jest liniami przerywanymi oraz podzielony ciągłymi liniami na wielokąty. W kolumnach oznaczono także białe paski, czyli miejsca na „słupki”, które należy oznaczyć tak, aby spełnione były następujące dwa warunki:
– każdy słupek powinien sięgać innej wysokości (środka kratki) oznaczonej liczbą z lewej strony diagramu – od 0 do 8 (zero jest brakiem słupka);
– cztery i tylko cztery kratki każdego wieloboku powinny znaleźć się w zasięgu słupków.
Przykład
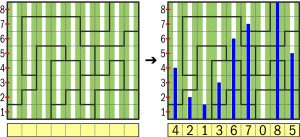
Zadanie
Końcowym rozwiązaniem jest ciąg liczb pod diagramem, oznaczających wysokości kolejnych słupków.

Komentarze
Rozwiązanie to 168327504.
Chyba idealny stopień trudności – jest satysfakcja z tzw. logicznego rozwiązania, ale też gdyby było trochę trudniejsze to „wyjadacze” mieliby więcej pola do popisu 😉
168327504
Pozdrawiam 😉
W przykładzie widzę dwie niezgodności z deklarowanymi zasadami:
– słupki 2 i 1 zajmują tylko 3 kratki goszczącego je wielokąta (istotna),
– słupki 1 i 8 są przeciągnięte do końca kratki (nieistotna).
Czy nie łatwiej byłoby rysować słupki i zliczać zajęte kratki, gdyby skala opisywała górne krawędzie kratek zamiast środków, a słupki też sięgały do końca krawędzi?
PS. Cofam pierwszą uwagę, jakoś przeoczyłem kratkę zajętą przez 4 🙁
Podtrzymuję uwagę kosmetyczną.
Mogę się zgodzić z uwagą kosmetyczną, bo zgoda buduje…
mp
168327504
168327504
http://pokazywarka.pl/fsc3oq/
_______________________________________________
Chyba poziom trudności jest OK, a zadanie znakomite.
Ta metoda może służyć do szyfrowania, tylko zastanawiam się nad jednoznacznością. W przykładzie można było zamienić 1 i 2.
Chyba trudno ustalić jakąś strategię poza ogólną „dopasowywania”, a to ze względu na przeróżne kształty obszarów i zależności między nimi.
Zgadzam się z apartado (piszę z małej litery bo taki jest nick), zadanie do trudnych nie należy. Podejrzewam, że trudność zadania zależy od sposobu „pokrojenia” diagramu. Rozwiązanie 168327504. Kiedy jest planowane wydanie Omnibusa ?
Z grubsza druga połowa czerwca. Dokładnego terminu jeszcze nie znam.
mp
168427504
Żeby uniknąć kłopotliwej ciszy zauważmy, że zadanie przykładowe ma dwa rozwiązania.
Istotnie, ale różnica jest jak uwaga Markoniusza – kosmetyczna.
mp
Na poniższej liście pozycja 14 jest rozwiązaniem zadania.
Pozostałe 80 pozycji to rozwiązania po odrzuceniu warunku różnej wysokości słupków.
Mówiąc szczerze zaskoczyło mnie, że jest ich aż tyle.
1,1,6,6,1,8,4,5,0,5
2,1,6,6,3,8,0,4,8,0
3,1,6,6,3,8,0,6,1,5
4,1,6,6,3,8,1,6,0,5
5,1,6,7,1,7,4,5,0,5
6,1,6,7,3,7,0,4,8,0
7,1,6,7,3,7,0,6,1,5
8,1,6,7,3,7,1,6,0,5
9,1,6,8,1,4,6,5,0,5
10,1,6,8,1,4,7,5,0,4
11,1,6,8,1,4,8,5,0,3
12,1,6,8,1,6,4,5,0,5
13,1,6,8,3,2,6,5,0,5
14,1,6,8,3,2,7,5,0,4
15,1,6,8,3,2,8,5,0,3
16,1,6,8,3,6,0,4,8,0
17,1,6,8,3,6,0,6,1,5
18,1,6,8,3,6,1,6,0,5
19,1,7,3,1,8,6,5,0,5
20,1,7,3,1,8,7,5,0,4
21,1,7,3,1,8,8,5,0,3
22,2,6,6,0,8,4,5,0,5
23,2,6,7,0,7,4,5,0,5
24,2,6,8,0,4,6,5,0,5
25,2,6,8,0,4,7,5,0,4
26,2,6,8,0,4,8,5,0,3
27,2,6,8,0,6,4,5,0,5
28,2,7,3,0,8,6,5,0,5
29,2,7,3,0,8,7,5,0,4
30,2,7,3,0,8,8,5,0,3
31,3,7,2,0,8,6,5,0,5
32,3,7,2,0,8,7,5,0,4
33,3,7,2,0,8,8,5,0,3
34,4,7,0,1,8,6,5,0,5
35,4,7,0,1,8,7,5,0,4
36,4,7,0,1,8,8,5,0,3
37,4,7,1,0,8,6,5,0,5
38,4,7,1,0,8,7,5,0,4
39,4,7,1,0,8,8,5,0,3
40,5,6,0,1,8,6,5,0,5
41,5,6,0,1,8,7,5,0,4
42,5,6,0,1,8,8,5,0,3
43,5,6,1,0,8,6,5,0,5
44,5,6,1,0,8,7,5,0,4
45,5,6,1,0,8,8,5,0,3
46,6,6,0,1,7,6,5,0,5
47,6,6,0,1,7,7,5,0,4
48,6,6,0,1,7,8,5,0,3
49,6,6,0,1,8,5,5,0,5
50,6,6,0,4,8,0,4,8,0
51,6,6,0,4,8,0,6,1,5
52,6,6,0,4,8,1,6,0,5
53,6,6,1,0,7,6,5,0,5
54,6,6,1,0,7,7,5,0,4
55,6,6,1,0,7,8,5,0,3
56,6,6,1,0,8,5,5,0,5
57,7,6,0,1,6,6,5,0,5
58,7,6,0,1,6,7,5,0,4
59,7,6,0,1,6,8,5,0,3
60,7,6,0,1,7,5,5,0,5
61,7,6,0,4,7,0,4,8,0
62,7,6,0,4,7,0,6,1,5
63,7,6,0,4,7,1,6,0,5
64,7,6,1,0,6,6,5,0,5
65,7,6,1,0,6,7,5,0,4
66,7,6,1,0,6,8,5,0,3
67,7,6,1,0,7,5,5,0,5
68,8,6,0,1,5,6,5,0,5
69,8,6,0,1,5,7,5,0,4
70,8,6,0,1,5,8,5,0,3
71,8,6,0,1,6,5,5,0,5
72,8,6,0,4,2,6,5,0,5
73,8,6,0,4,2,7,5,0,4
74,8,6,0,4,2,8,5,0,3
75,8,6,0,4,6,0,4,8,0
76,8,6,0,4,6,0,6,1,5
77,8,6,0,4,6,1,6,0,5
78,8,6,1,0,5,6,5,0,5
79,8,6,1,0,5,7,5,0,4
80,8,6,1,0,5,8,5,0,3
81,8,6,1,0,6,5,5,0,5
Dla wszystkich co zrobili zadanie domowe proponuję zadanie z gwiazdką:
Znajdź taki różnowartościowy układ słupków aby każdy obszar był „nadgryziony” przez słupki w innym stopniu. Nie narzucamy przy tym warunku, że liczby maja być z przedziału (0..8)
A więc zmieniamy drugi warunek, który mówił, że każdy obszar miał być „nadgryziony” przez słupki w ilości 4 kratek.
To jest chyba dużo trudniejsze dla człowieka niż zadanie pierwotne ?
Dla maszyny jest to ten sam poziom trudności.
Widzę, że majowa pogoda nie sprzyja łamigłówkom nadliczbowym ale skoro wywołałem wilka z lasu to teraz wypada go tam z powrotem zapędzić 😉
Otóż na postawione we wpisie 192665 zadanie jest następująca odpowiedź. Używając retoryki klasyka można powiedzieć, że rozwiązanie jest jedno a nawet cztery.
Wynika to stąd, że otrzymujemy jedną kombinację różnowartościową dla obszarów ale odpowiadają jej aż cztery różnowartościowe kombinacje dla słupków.
26,0,7,1,2,3,4,6,8,5,”*”,0,8,4,1,7,2,5,3,6
27,0,7,1,2,4,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
48,1,7,0,2,3,4,6,8,5,”*”,0,8,4,1,7,2,5,3,6
49,1,7,0,2,4,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
Jeśli odrzucimy warunek różnowartościowości dla słupków to mamy 84 takich, gorszych, rozwiązań.
Poniżej pełna lista rozwiązań pierwszego i drugiego sortu razem 😉
1,0,5,3,2,3,4,6,8,5,”*”,0,8,2,1,7,4,5,3,6
2,0,5,3,2,4,3,6,8,5,”*”,0,8,2,1,7,4,5,3,6
3,0,5,3,3,3,3,6,8,5,”*”,0,8,2,1,7,4,5,3,6
4,0,5,3,6,5,7,6,8,5,”*”,1,9,2,8,7,4,5,3,6
5,0,5,3,6,5,8,6,7,5,”*”,1,9,2,8,7,4,5,3,6
6,0,5,3,6,5,8,6,8,4,”*”,1,9,2,8,7,4,5,3,6
7,0,5,3,6,5,8,6,8,5,”*”,1,10,2,8,7,4,5,3,6
8,0,5,4,2,3,3,6,8,5,”*”,0,8,2,1,7,4,5,3,6
9,0,5,4,5,5,7,6,8,5,”*”,1,9,2,8,7,4,5,3,6
10,0,5,4,5,5,8,6,7,5,”*”,1,9,2,8,7,4,5,3,6
11,0,5,4,5,5,8,6,8,4,”*”,1,9,2,8,7,4,5,3,6
12,0,5,4,5,5,8,6,8,5,”*”,1,10,2,8,7,4,5,3,6
13,0,5,4,6,4,7,6,8,5,”*”,1,9,2,8,7,4,5,3,6
14,0,5,4,6,4,8,6,7,5,”*”,1,9,2,8,7,4,5,3,6
15,0,5,4,6,4,8,6,8,4,”*”,1,9,2,8,7,4,5,3,6
16,0,5,4,6,4,8,6,8,5,”*”,1,10,2,8,7,4,5,3,6
17,0,5,4,6,5,5,6,8,5,”*”,0,8,2,9,7,4,5,3,6
18,0,5,4,6,5,6,6,8,5,”*”,1,8,2,9,7,4,5,3,6
19,0,5,4,6,5,7,6,7,5,”*”,1,8,2,9,7,4,5,3,6
20,0,5,4,6,5,7,6,8,4,”*”,1,8,2,9,7,4,5,3,6
21,0,5,4,6,5,8,6,6,5,”*”,1,8,2,9,7,4,5,3,6
22,0,5,4,6,5,8,6,7,4,”*”,1,8,2,9,7,4,5,3,6
23,0,5,4,6,5,8,6,8,3,”*”,1,8,2,9,7,4,5,3,6
24,0,5,4,6,5,8,6,8,5,”*”,1,10,2,9,7,4,5,3,6
25,0,5,4,6,6,5,6,8,5,”*”,1,8,2,9,7,4,5,3,6
26,0,7,1,2,3,4,6,8,5,”*”,0,8,4,1,7,2,5,3,6
27,0,7,1,2,4,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
28,0,7,1,3,3,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
29,0,7,1,6,5,7,6,8,5,”*”,1,9,4,8,7,2,5,3,6
30,0,7,1,6,5,8,6,7,5,”*”,1,9,4,8,7,2,5,3,6
31,0,7,1,6,5,8,6,8,4,”*”,1,9,4,8,7,2,5,3,6
32,0,7,1,6,5,8,6,8,5,”*”,1,10,4,8,7,2,5,3,6
33,0,7,5,0,2,3,6,8,5,”*”,0,8,5,1,7,4,3,2,6
34,1,5,2,2,3,4,6,8,5,”*”,0,8,2,1,7,3,5,4,6
35,1,5,2,2,4,3,6,8,5,”*”,0,8,2,1,7,3,5,4,6
36,1,5,2,3,3,3,6,8,5,”*”,0,8,2,1,7,3,5,4,6
37,1,5,2,6,5,7,6,8,5,”*”,1,9,2,8,7,3,5,4,6
38,1,5,2,6,5,8,6,7,5,”*”,1,9,2,8,7,3,5,4,6
39,1,5,2,6,5,8,6,8,4,”*”,1,9,2,8,7,3,5,4,6
40,1,5,2,6,5,8,6,8,5,”*”,1,10,2,8,7,3,5,4,6
41,1,6,1,2,3,4,6,8,5,”*”,0,8,3,1,7,2,5,4,6
42,1,6,1,2,4,3,6,8,5,”*”,0,8,3,1,7,2,5,4,6
43,1,6,1,3,3,3,6,8,5,”*”,0,8,3,1,7,2,5,4,6
44,1,6,1,6,5,7,6,8,5,”*”,1,9,3,8,7,2,5,4,6
45,1,6,1,6,5,8,6,7,5,”*”,1,9,3,8,7,2,5,4,6
46,1,6,1,6,5,8,6,8,4,”*”,1,9,3,8,7,2,5,4,6
47,1,6,1,6,5,8,6,8,5,”*”,1,10,3,8,7,2,5,4,6
48,1,7,0,2,3,4,6,8,5,”*”,0,8,4,1,7,2,5,3,6
49,1,7,0,2,4,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
50,1,7,0,3,3,3,6,8,5,”*”,0,8,4,1,7,2,5,3,6
51,1,7,0,6,5,7,6,8,5,”*”,1,9,4,8,7,2,5,3,6
52,1,7,0,6,5,8,6,7,5,”*”,1,9,4,8,7,2,5,3,6
53,1,7,0,6,5,8,6,8,4,”*”,1,9,4,8,7,2,5,3,6
54,1,7,0,6,5,8,6,8,5,”*”,1,10,4,8,7,2,5,3,6
55,2,5,2,1,3,4,6,8,5,”*”,0,8,2,1,7,3,4,5,6
56,2,5,2,1,4,3,6,8,5,”*”,0,8,2,1,7,3,4,5,6
57,2,5,2,2,2,4,6,8,5,”*”,0,8,2,1,7,3,4,5,6
58,2,5,2,3,2,3,6,8,5,”*”,0,8,2,1,7,3,4,5,6
59,2,5,3,1,2,4,6,8,5,”*”,0,8,2,1,7,4,3,5,6
60,2,5,4,1,2,3,6,8,5,”*”,0,8,2,1,7,4,3,5,6
61,2,6,0,2,3,4,6,8,5,”*”,0,8,3,1,7,2,5,4,6
62,2,6,0,2,4,3,6,8,5,”*”,0,8,3,1,7,2,5,4,6
63,2,6,0,3,3,3,6,8,5,”*”,0,8,3,1,7,2,5,4,6
64,2,6,0,6,5,7,6,8,5,”*”,1,9,3,8,7,2,5,4,6
65,2,6,0,6,5,8,6,7,5,”*”,1,9,3,8,7,2,5,4,6
66,2,6,0,6,5,8,6,8,4,”*”,1,9,3,8,7,2,5,4,6
67,2,6,0,6,5,8,6,8,5,”*”,1,10,3,8,7,2,5,4,6
68,2,6,1,1,3,4,6,8,5,”*”,0,8,3,1,7,2,4,5,6
69,2,6,1,1,4,3,6,8,5,”*”,0,8,3,1,7,2,4,5,6
70,2,6,1,2,2,4,6,8,5,”*”,0,8,3,1,7,2,4,5,6
71,2,6,1,3,2,3,6,8,5,”*”,0,8,3,1,7,2,4,5,6
72,2,7,1,1,2,4,6,8,5,”*”,0,8,4,1,7,2,3,5,6
73,3,5,0,2,3,4,6,8,5,”*”,0,8,2,1,7,3,5,4,6
74,3,5,0,2,4,3,6,8,5,”*”,0,8,2,1,7,3,5,4,6
75,3,5,0,3,3,3,6,8,5,”*”,0,8,2,1,7,3,5,4,6
76,3,5,0,6,5,7,6,8,5,”*”,1,9,2,8,7,3,5,4,6
77,3,5,0,6,5,8,6,7,5,”*”,1,9,2,8,7,3,5,4,6
78,3,5,0,6,5,8,6,8,4,”*”,1,9,2,8,7,3,5,4,6
79,3,5,0,6,5,8,6,8,5,”*”,1,10,2,8,7,3,5,4,6
80,3,5,1,1,3,4,6,8,5,”*”,0,8,2,1,7,3,4,5,6
81,3,5,1,1,4,3,6,8,5,”*”,0,8,2,1,7,3,4,5,6
82,3,5,1,2,2,4,6,8,5,”*”,0,8,2,1,7,3,4,5,6
83,3,5,1,3,2,3,6,8,5,”*”,0,8,2,1,7,3,4,5,6
84,3,5,2,1,2,4,6,8,5,”*”,0,8,2,1,7,4,3,5,6
85,3,5,3,0,2,4,6,8,5,”*”,0,8,2,1,7,5,3,4,6
86,3,5,4,0,2,3,6,8,5,”*”,0,8,2,1,7,5,3,4,6
87,4,5,1,1,2,4,6,8,5,”*”,0,8,2,1,7,4,3,5,6
88,4,5,2,0,2,4,6,8,5,”*”,0,8,2,1,7,5,3,4,6
Zadanie bardzo spokrewnione z TERMOMETRAMI z 30 marca 2016.
Przy czym słupki na pozór trudniejsze, bo nieco większa plansza i obszary obejmują kilka wierszy i kolumn na raz, okazały się o wiele łatwiejsze, dla komputera, od termometrów, których było aż 21, chociaż miały mniejsze wartości.