Kłamigłówka

24 marca 2018
Marek Penszko

Łamigłówki, w których pojawiają się „kłamstwa”, nie są nowością. Mistrzem w konstruowaniu takich logicznych zadań tekstowych był zmarły przed rokiem Raymond Smullyan. W jego książkach z zagadkami, których kilka ukazało się w Polsce, często pojawiają się kłamcy i prawdomówni, a istotę rozwiązania stanowi m. in. ustalenie, kto jest kim.
Znacznie rzadsze są diagramowe zadania z kłamczuszkami. Chyba już jakieś pojawiały się w Łamiblogu, ale nie mam pewności czy i kiedy, bo gubię się w swoich wpisach, których liczba dobiega tysiąca. Na pewno jednak dotąd nie prezentowałem poniższego, które wydaje się całkiem urokliwe.

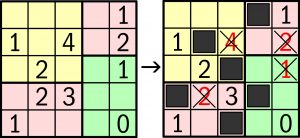
Niektóre kratki diagramu należy zaczernić. Kluczem do tego są cyfry. Prawie każda oznacza, ile pustych (bez cyfry) kratek, sąsiadujących bokiem z polem z cyfrą, powinno zmienić się w czarne. Prawie, ponieważ jedna i tylko jedna cyfra w każdej kolorowej działce „kłamie”, czyli nie oznacza tego, co – zgodnie z poprzednim zdaniem – powinna. Które cyfry są kłamczuszkami, to trzeba oczywiście ustalać samemu w trakcie rozwiązywania.
I jeszcze dwa ważne warunki: zaczernione pola nie mogą stykać się bokami, a stykając się rogami nie mogą odcinać kawałków diagramu, czyli dzielić go na części.

Przykład:

Zadanie:

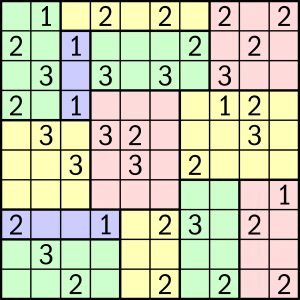
W rozwiązaniu wystarczy podać liczbę zaczernionych kratek.