96
Od roku bez mała jestem molestowany w sprawie pewnego zadania. Ułożył je mój kolega, rzec by można – po fachu, choć bardziej pasowałoby – po zamiłowaniu, poniekąd z mojej inspiracji – i wytrwale przy każdej okazji namawia mnie do zamieszczenia owego dziełka w Łamiblogu. To rodzaj łamigłówki, który lubię i cenię – z japońskim rodowodem, goszczący tu zresztą już chyba dwu- lub trzykrotnie. Problem w tym, że zadanie wydaje mi się katorżnicze. Z drugiej jednak strony mam szansę uniknąć dalszego molestowania, decydując się na pomolestowanie gości Łamibloga. Nie wydaje mi się to zresztą zbyt okrutne, bo Państwo mogą po prostu rozwiązywanie sobie odpuścić. A zatem do rzeczy.
Chodzi o okaz zwany „Cyframi do strzałek” lub „Japońskimi strzałkami”. Przypominam krótką, zakręconą instrukcję:
Do każdej kratki należy wpisać taką cyfrę – z zakresu od 1 do 9 – aby strzałka w kratce X wskazywała na kratki z tyloma różnymi cyframi, jaka jest wartość cyfry w kratce X. Na dobry początek dwie cyfry są na swoich miejscach.
Gwoli jasności najpierw przykład z mniejszym zakresem cyfr.
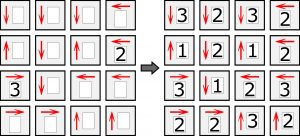
A oto 100-strzałkowy „potwór”.
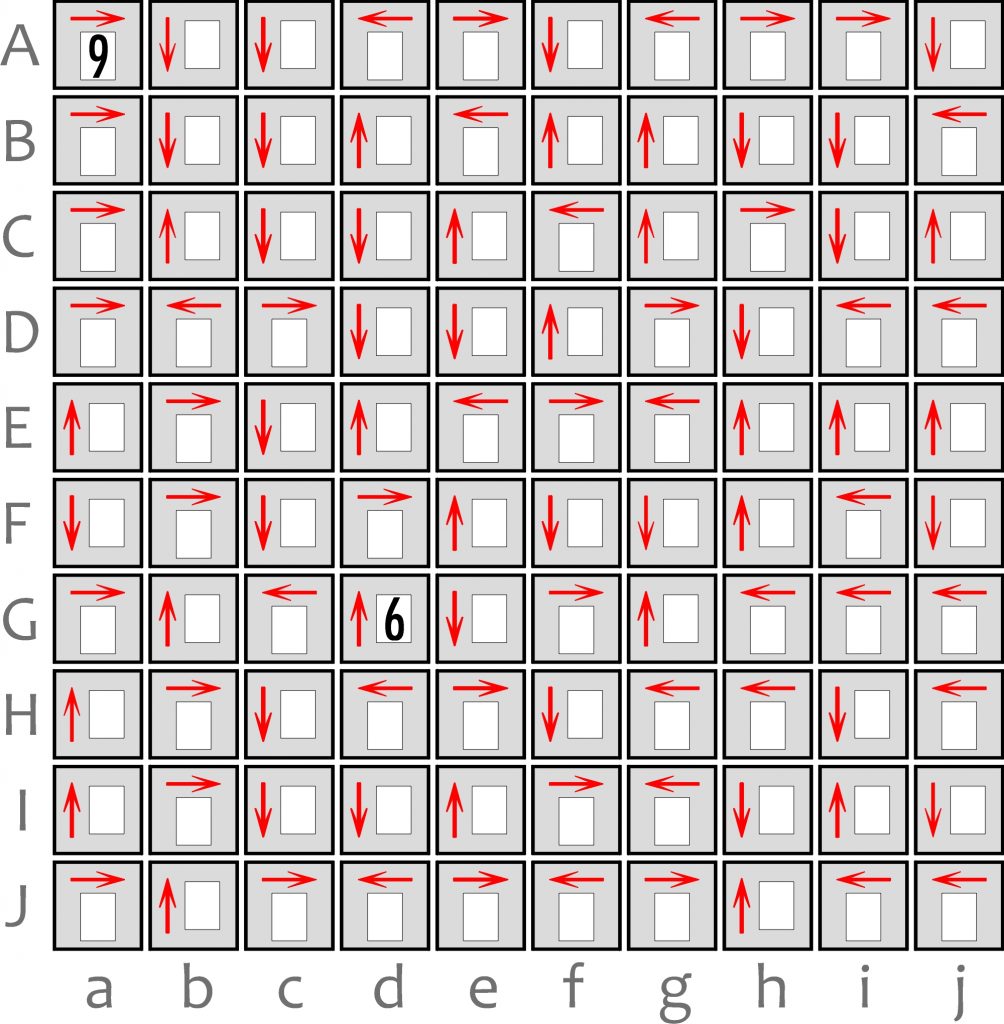
Oznaczyłem współrzędne na wypadek, gdyby pojawiły się jakieś uwagi, dotyczące konkretnych pól lub toku rozwiązywania.
Jeśli komuś starczy czasu i wytrwałości, czyli nie tylko zdecyduje się zacząć, ale słaniając się resztką sił dotrze do końca, to proszę chociaż o informację, w ilu kratkach pojawiły się piątki.

Komentarze
czy da się to rozwiązać „na logikę” bez zgadywania? wpisałem 25 cyfr a dalej ani rusz :/
Zdaniem autora zadania – da się.
mp
http://pokazywarka.pl/ag4776/
Ja to nawet lubię takie zadania. Wypoczywam przy nich. Moja rodzina tego pojąć nie może, ale tutaj pewnie ktoś się znajdzie 😉
Logika jest jak najbardziej uzasadniona.
Wystarczy skorzystać ze wzoru:
tytuł wpisu : (ilość różnych cyfr do wpisania – ilość cyfr, które nas interesują) = w tylu kratkach otrzymamy naszą poszukiwaną cyfrę
Pozwoliłem sobie na taki mały żarcik, bo przypomniał mi się pewien artykuł, który dawno temu przeglądałem. A teza tego artykułu była następująca:
Na podstawie numeru dowodu osobistego wszystko da się wykazać.
Drobne uściślenie informacji, podanych w pierwszych dwóch zdaniach opisu zadania. Otóż nie jestem w pełni autorem tego zadania, a raczej jego „rekonstruktorem”. Gospodarz Łamibloga miał w swoim archiwum rozwiązanie zadania ze strzałkami 10×10, ale nie miał wyjściowego diagramu. Zwrócił się wiec do mnie z zapytaniem, czy byłbym w stanie (a raczej czy byłby w stanie mój komputer) odtworzyć wygląd wyjściowego diagramu. Usuwając kolejne cyfry, doszedłem do zaskakującego wniosku, że do jednoznacznego rozwiązania wystarczy pozostawienie tylko dwóch ujawnionych. (Nawiasem mówiąc jednoznaczne rozwiązanie pozostaje nawet wtedy, gdy z diagramu usunie się 7 strzałek.)
Nie wiem, jaki był diagram oryginalnego zadania, ale uważam, że to co udało mi się zrobić, wyszło całkiem nieźle.
Oczywiście to, że komputer zadanie rozwiązał, nie wystarczy do opublikowania go w Łamiblogu, który przecież przeznaczony jest dla ludzi. Dlatego spróbowałem rozwiązać zadanie „na kartce”. I okazało się, że da się rozwiązać praktycznie samą logiką.
Logiką wpisałem 34 cyfry. Dalej nic nie mogę wymyślić. Oczywiście można zaprząc do pracy komp, ale to nie o to chodzi.
Ponieważ się spóźniłem więc nie podaję rozwiązania 🙂 ale zauważę tylko,
że mimo, iż zadanie wymagało więcej przebiegów programu, to okazało się łatwiejsze od zadania z wpisu z 7 listopada 2016 w tym sensie, że w tamtym zadaniu nie dało się ustalić jednoznacznie wszystkich wierszy/kolumn i potrzebny był ostatni etap poszukiwań, który w tym zadaniu nie był konieczny.
@ OlaGM & Michał S:
Czy istnieje ścieżka na której w każdym rozgałęzieniu (a chyba składa się ona z samych rozgałęzień) możemy uniknąć benedyktyńskiego sprawdzania wielu możliwości ???
Ja zrezygnowałem z ręcznej roboty po wpisaniu do każdej kratki maksymalnej możliwej liczby (ilość kratek od grota do ściany) a następnie poprawieniu tych wyników w przypadkach powtarzania się odpowiednio dużej ilości liczb w rzędzie. Może jest tu jakiś pomysł, którego nie widzę ?
@Spytko
Nie wiem, czy istnieje ścieżka bez odgałęzień. Sprawdzałam daną możliwość, a jak się spsiła, tzn. doprowadziła do sprzeczności, to ją wymazywałam. Po czym brałam się za następną. Robota pedantyczna, ale nie nużąca na tyle, żeby porzucić. Diagram wypełniał się krok po kroku.
Moim zdaniem „benedyktyńskie sprawdzanie wielu możliwości” nie jest w tym zadaniu konieczne. Z tym, że ja do każdej kratki wpisywałem ograniczenia zarówno od góry, jak i od dołu, co z kolei często prowadziło do redukcji zakresu możliwości w innych kratkach. Liczba kratek „do ściany” nie jest jedynym ograniczeniem z góry. Popatrzmy np. na kratkę Cd. Z odległości od ściany wynika, że jej maksimum to 7. Ale w kolumnie d, poniżej Cd, wszystkie kratki mają maksimum najwyżej 6, a więc w Cd też musi być maksimum 6.
Rozwiązywanie tego zadania w dużym stopniu opiera się na spostrzegawczości. Np. od razu można wpisać wszystkie cyfry w rzędzie A oraz w kolumnie d powyżej ujawnionej cyfry 6. Istotne jest też szybkie zauważenie, że w kolumnie j cyfra 9 musi być w kratce Dj, bo to od razu pozwala na wpisanie w rzędzie D prawie wszystkich cyfr (zostają tylko kratki De i Dh – w jednej z nich musi być 4, a w drugiej 6). Gdy w dalszym toku rozwiązywania dojdziemy do Gj=8, to jedynym miejscem na cyfrę 1 w rzędzie G będzie Ge itd.
@ OlaGM & Michał S:
Inną mocną cechą jest to, że liczby w kratkach ze strzałkami o tym samym zwrocie tworzą ciąg niemalejący ().
Ale mnie to zadanie kojarzy się z przede wszystkim z mozołem.
W żadnym z trzech zadań, goszczących na blogu, nie pojawił się moment przełomu, po którym proces wyraźnie przyśpieszał, no może sama końcówka. Za to napisanie programu jak najbardziej daje satysfakcję, bo komputer jest właśnie od radzenia sobie z taką monotonną materią.
@ Spytko z Melsztyna:
Jeśli chodzi o strzałki o zgodnych zwrotach, to jest jeszcze druga istotna własność: różnica między cyframi nie może być większa niż odległość zawierających je komórek. Stąd od razu widać, że np. w komórce Ae musi być cyfra 5.
Inna ciekawa własność związana jest ze strzałkami o przeciwnych zwrotach, znajdującymi się w przeciwnych końcach wiersza lub kolumny (tak jest np. w wierszach B, D, G, J oraz kolumnie b). Różnica cyfr w tych krańcowych komórkach nie może być większa niż 1.
Zadanie dodatkowe na dzisiejszy wieczór 🙂
Jaka jest minimalna liczba strzałek i jak muszą być umieszczone w wierszu aby można było jednoznacznie wpisać wszystkie liczby ?