Znaki działają
W przeciwieństwie do dwóch poprzednich wpisów miało być tym razem normalnie, czyli zadanie z pełną instrukcją. Ale nie jest. Głównie dlatego, że zasmakowałem w takich jakby podwójnych łamigłówkach diagramowych zwanych indukcyjnymi, których rozwiązanie wymaga najpierw wywnioskowania z przykładu, co trzeba zrobić – a potem z tego skorzystać. Ponadto w tym przypadku łatwo zauważyć, że podstawowym celem jest stary znajomy – kwadrat łaciński.
Przykład z rozwiązaniem wygląda tak:
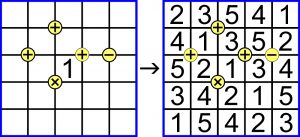
Rozszyfrowanie instrukcji sprowadza się więc w gruncie rzeczy do ustalenia, jak działają znaki działania na styku czterech pól, a właściwie czterech cyfr. Zaś po uporaniu się z instrukcją (to jest jednak dość proste) pora powalczyć z zadaniem (to wydaje się znacznie trudniejsze):
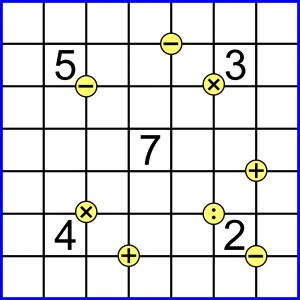
W rozwiązaniu wystarczy podać pierwszą kolumnę siedmiu cyfr – kolejno od góry do dołu.

Komentarze
6142573
Pozdrawiam 😉
Nie jest zbyt trudne
6143572
1572634
4756213
2317456
5234167
7465321
3621745
Przykład nie daje jednoznaczności nastepującej reguły.
Mamy kafelek
AB
CD
ze znakiem +,-,*,: pośrodku.
Wydaje się, że reguła jest następująca:
Dla dodawania A+D=B+C
Dal mnożenia A*D=B*C
Dla odejmowania A-D=C-B ale mogłoby być również ABS(A-D)=ABS(B-C) (wersja słaba)
Dla dzielenia jeśli dosłownie przenieść z odejmowania (wersja mocna) to musiałoby być A:D=C:B
ale można by dopuścić również, że wystarczy spełnienie jednej z 4 możliwości wiadomo jakich (wersja słaba).
Pytanie brzmi, czy mamy do czynienia z wersją:
a) mocną
b) słabą
c) jeszcze inną ?
Samemu trzeba sobie odpowiedzieć, próbując rozwiązać zadanie.
mp
Kurcze! Ja już chyba pisałem, że nie lubię zadań indukcyjnych… 🙁
Ciężkie 🙂 Bez strzelania się nie obyło.
Zasady: w kwadracie wokół znaku działania stosujemy działanie dla cyfr leżących w przeciwległych wierzchołkach, w ten sposób, że wynik działania jest taki sam w obu parach.
6143572
1572634
4756213
2317456
5234167
7465321
3621745
Mam wątpliwość co do czterech cyfr z prawego, dolnego rogu:
jest tam odejmowanie, ale w tym jedynym przypadku działanie trzeba by wykonać odrobinę łamiąc instrukcję:
„wynik działania na cyfrach po przekątnej jest taki sam dla obu przekątnych/ od lewej do prawej”
A może jednak taki układ „działa”?
6 1 4 3 5 7 2
1 5 7 2 6 3 4
4 7 5 6 2 1 3
2 3 1 7 4 5 6
5 2 3 4 1 6 7
7 4 6 5 3 2 1
3 6 2 1 7 4 5
6142573
Drugie rozwiązanie- 3142576
Pomyłka, drugie rozwiązanie błedne
Uff ale orka … Ale fajne!
6435712.
Pozdrawiam z Krakowa.
6142573
Nie wiem, czy zdążę… pierwsza część, by zaznaczyć obecność: działanie ma dać ten sam wynik na liczbach z przekątnych wokół znaku, jak w przykładzie 3+3 = 1+5, 5-4 = 3-2, etc.
Pomyliłem jedną cyfrę w programie …….ale już się doliczył i nie chce być inaczej niż jest 😉