Talizmagia

8 września 2016
Marek Penszko

Figury magiczne i talizmanowe już się w Łamiblogu pojawiały, ale takie, które byłyby równocześnie magiczne i talizmanowe – jeszcze nie. Czy się pojawią, to zależy od Państwa. Konkretnie chodzi o magiczno-talizmanowe kwadraty 4×4.

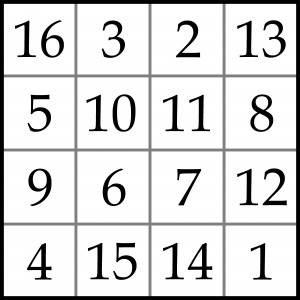
Różnych (z dokładnością do obrotów i odbić lustrzanych) kwadratów magicznych 4×4 jest 880. Najbardziej znany to „Melancholijny” kwadrat Dürera:

Tal_1

Czy jest on talizmanowy? Odpowiedź wymaga sprawdzenia, jakie są w tym kwadracie różnice między liczbami w sąsiednich polach (także stykających się tylko rogami), a ściślej, jaka jest najmniejsza z tych różnic R(min). Jak widać R(min) równa jest 1, a takich różnic jest aż osiem (3-2, 11-10, 7-6, 15-14, 6-5, 10-9, 8-7, 12-11). Gdybyśmy mieli pewność że w kwadracie magicznym 4×4 R(min) nie może być większa niż 1, to kwadrat Dürera byłby talizmanowy. A zatem kwadrat jest talizmanowy wówczas, gdy różnica R(min) jest największą możliwą.

Czy komuś z Państwa uda się znaleźć na piechotę kwadrat magiczny 4×4 z R(min)=2? Wątpię, bo to zajęcie benedyktyńskie, choć jestem prawie pewien, że takowy istnieje. Jednak znacznie mocniej wątpię w to, że R(min) może być równe 3, choć mam nadzieję, że sprawę ostatecznie rozstrzygną programiści, których wśród gości Łamibloga nie brakuje i już nieraz gospodarza wspierali. A może komuś uda się dowieść, że R(min)=3 w kwadracie 4×4 nie jest możliwe.

Kom