Talizmanowo

8 lipca 2016
Marek Penszko

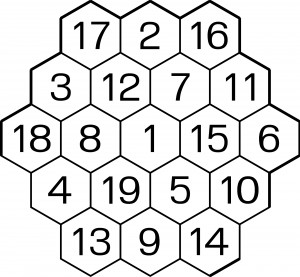
W encyklopedii matematycznej MathWorld znajduje się hasło „sześciokąt talizmanowy” zilustrowane następującym przykładem:

Tal_1

Ogólna matematyczna definicja takiego „zębatego” sześciokąta, stanowiącego fragment siatki heksagonalnej, podana jest w encyklopedii. Przykładowy składa się z 19 pól, w których rozmieszczono liczby od 1 do 19 tak, że – na tym polega jego „talizmanowość” – różnica między liczbami w sąsiednich polach nigdzie nie jest mniejsza od określonej liczby, w tym przypadku od 4.

Talizmanowe sześciokąty wymyślił i nazwał Joseph Madachy, spec od matematyki rekreacyjnej. Przykład pochodzi z jego książki wydanej w roku 1979. Od tego czasu nikt się takimi figurami liczbowymi bliżej nie interesował, więc postanowiłem dołożyć do tematu małą cegiełkę, zamieszczając w czerwcowym Świecie Nauki zadanie, polegające na wypełnieniu 19-polowego sześciokąta liczbami od 1 do 19 tak, aby różnica między liczbami w sąsiednich polach prawie nigdzie nie była mniejsza niż 5. Dopisałem „prawie”, bo początkowo sądziłem, że przykład w MathWorldzie jest ekstremalny i nie sposób go przebić, czyli wszystkich różnic nie mniejszych niż 5 nie idzie uzyskać. Tymczasem ku mojemu zdziwieniu okazało się to możliwe. Czy Państwu też uda się przebić MathWorlda? Nie wiem, na ile całkowicie różnych sposobów da się to zrobić, ale na pewno na więcej niż jeden.

Kom