Łożysko
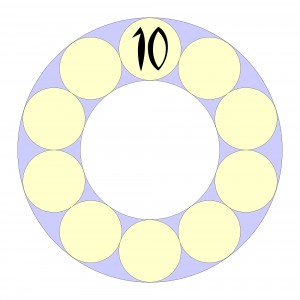
Dziesiątka jest na właściwym miejscu, a cyfry od 1 do 9 należy rozmieścić w pustych kulkach tak, aby spełniony był warunek, o którym za chwilę.
Gdy cyfry zostaną już rozmieszczone, będziemy dodawać każde dwie sąsiednie, zapisując sumy obok nich. Jakie powinno być rozmieszczenie cyfr, aby różnych sum wśród dziesięciu zapisanych było jak najmniej?

Komentarze
Załóżmy, że obok liczby 10 umieszczamy liczby a i b, oraz dodatkowo b>a. Nie ponadto drugą liczbą sąsiadującą z liczbą a będzie liczba x.
Mamy zatem fragment ciągu: b, 10, a, x
W tym fragmencie występują trzy sumy: b+10, 10+a, a+x, przy czym: b+10>10+a>a+x, bowiem b>a oraz 10>x.
To oznacza, że minimalna liczba różnych sum to 3. Można ją dość łatwo zrealizować, np. tak: 10, 1, 9, 2, 8, 3, 7, 4, 6, 5. Wtedy mamy tylko trzy różne sumy: 10, 11, 15.
Oto lista wszystkich układów, które generują trzy różne sumy:
10, 1, 2, 9, 4, 7, 6, 5, 8, 3
10, 1, 4, 7, 8, 3, 2, 9, 6, 5
10, 1, 6, 5, 2, 9, 8, 3, 4, 7
10, 1, 6, 5, 7, 4, 8, 3, 9, 2
10, 1, 6, 7, 4, 9, 2, 5, 8, 3
10, 1, 7, 4, 9, 2, 6, 5, 8, 3
10, 1, 8, 3, 6, 5, 4, 7, 2, 9
10, 1, 8, 3, 6, 5, 9, 2, 7, 4
10, 1, 8, 3, 6, 9, 2, 7, 4, 5
10, 1, 8, 4, 7, 5, 6, 3, 9, 2
10, 1, 8, 5, 4, 9, 2, 7, 6, 3
10, 1, 9, 2, 8, 3, 7, 4, 6, 5
10, 1, 9, 2, 8, 5, 6, 4, 7, 3
10, 1, 9, 3, 7, 5, 6, 4, 8, 2
10, 2, 8, 4, 6, 5, 7, 3, 9, 1
10, 2, 9, 3, 6, 5, 7, 4, 8, 1
10, 2, 9, 3, 8, 4, 7, 5, 6, 1
10, 3, 6, 7, 2, 9, 4, 5, 8, 1
10, 3, 7, 4, 6, 5, 8, 2, 9, 1
10, 3, 8, 5, 2, 9, 4, 7, 6, 1
10, 3, 8, 5, 6, 2, 9, 4, 7, 1
10, 3, 8, 5, 6, 7, 4, 9, 2, 1
10, 4, 7, 2, 9, 5, 6, 3, 8, 1
10, 5, 4, 7, 2, 9, 6, 3, 8, 1
10, 5, 6, 4, 7, 3, 8, 2, 9, 1
10, 5, 6, 9, 2, 3, 8, 7, 4, 1
10, 7, 4, 3, 8, 9, 2, 5, 6, 1
10, 9, 2, 7, 4, 5, 6, 3, 8, 1
I jeszcze informacja ile permutacji liczba od 1 do 9 daje n różnych sum:
3: 28
4: 504
5: 7320
6: 40572
7: 109056
8: 127928
9: 66580
10: 10892
Wpadłem na jeszcze jedno proste uzasadnienie, że muszą wystąpić przynajmniej trzy różne sumy.
Liczba 10 ze swoimi sąsiadami tworzy dwie różne sumy większe od 10. Natomiast liczba 1 z mniejszym sąsiadem tworzy sumę równą co najwyżej 10. Mamy zatem 3 różne sumy.
Z tego uzasadnienia wynika również, że jeśli liczby 1 i 10 nie są sąsiadami, to będą przynajmniej 4 różne sumy: dwie większe od 10 (liczba 10 z sąsiadami) oraz dwie równe co najwyżej 10 (liczba 1 z sąsiadami).
Ładne. Gdyby dodać warunek 1a, że suma (najmniejszej liczby) różnych sum powinna być największa, to byłoby jedno rozwiązanie?
mp
Gdy wpiszemy kolejno 10,1,9,2,8,3,7,4,6,5 mamy trzy sumy 10,11 i 15
Zarówno największa (39), jak i najmniejsza (27) suma sum występują w podanych rozwiązaniach dokładnie dwukrotnie, przy czym podana przeze mnie lista rozwiązań uwzględnia orientację, tzn. rozwiązania symetryczne pojawiają się na niej dwukrotnie.
A zatem tak: dodanie warunku 1a sprawia, że zadanie ma jedno rozwiązanie.
Dość proste do skonstruowania ręcznego:
10,9,2,7,4,5,6,3,8,1 różnych sum: 3 => 9,11,19
Trudniejsze do znalezienia:
10,2,9,3,8,4,7,5,6,1 różnych sum: 3 => 7,11,12
Nieoczywiste:
10,2,9,3,6,5,7,4,8,1 różnych sum: 3 => 9,11,12
http://i.imgur.com/BfLBut8.png
Dość łatwe zadanie, wystarczy 9 dać po przeciwnej stronie 10 i starać się zachować sumy takie jak po przeciwnej stronie łożyska.
1 2 9 4 7 6 5 8 3 10
1 4 7 8 3 2 9 6 5 10
1 6 5 2 9 8 3 4 7 10
1 6 5 7 4 8 3 9 2 10
1 6 7 4 9 2 5 8 3 10
1 7 4 9 2 6 5 8 3 10
1 8 3 6 5 4 7 2 9 10
1 8 3 6 5 9 2 7 4 10
1 8 3 6 9 2 7 4 5 10
1 8 4 7 5 6 3 9 2 10
1 8 5 4 9 2 7 6 3 10
1 9 2 8 3 7 4 6 5 10
1 9 2 8 5 6 4 7 3 10
1 9 3 7 5 6 4 8 2 10
2 8 4 6 5 7 3 9 1 10
2 9 3 6 5 7 4 8 1 10
2 9 3 8 4 7 5 6 1 10
3 6 7 2 9 4 5 8 1 10
3 7 4 6 5 8 2 9 1 10
3 8 5 2 9 4 7 6 1 10
3 8 5 6 2 9 4 7 1 10
3 8 5 6 7 4 9 2 1 10
4 7 2 9 5 6 3 8 1 10
5 4 7 2 9 6 3 8 1 10
5 6 4 7 3 8 2 9 1 10
5 6 9 2 3 8 7 4 1 10
7 4 3 8 9 2 5 6 1 10
9 2 7 4 5 6 3 8 1 10
Gdyby dosłownie przyjąć słowo „cyfry” z treści zadania, to zamiast 10 można wpisać 0:
1 8 3 6 5 4 7 2 9 0
3 6 7 2 1 8 5 4 9 0
5 4 1 8 7 2 3 6 9 0
5 4 6 3 7 2 8 1 9 0
5 6 3 8 1 4 7 2 9 0
6 3 8 1 5 4 7 2 9 0
7 2 5 4 3 6 1 8 9 0
7 2 5 4 8 1 6 3 9 0
7 2 5 8 1 6 3 4 9 0
7 3 6 4 5 2 8 1 9 0
7 4 3 8 1 6 5 2 9 0
8 1 7 2 6 3 5 4 9 0
8 1 7 4 5 3 6 2 9 0
8 2 6 4 5 3 7 1 9 0
9 1 7 3 5 4 6 2 8 0
9 1 8 2 5 4 6 3 7 0
9 1 8 2 7 3 6 4 5 0
9 2 5 6 1 8 3 4 7 0
9 2 6 3 5 4 7 1 8 0
9 2 7 4 1 8 3 6 5 0
9 2 7 4 5 1 8 3 6 0
9 2 7 4 5 6 3 8 1 0
9 3 6 1 8 4 5 2 7 0
9 4 3 6 1 8 5 2 7 0
9 4 5 3 6 2 7 1 8 0
9 4 5 8 1 2 7 6 3 0
9 6 3 2 7 8 1 4 5 0
9 8 1 6 3 4 5 2 7 0
Rozwiązanie: 10,1,9,3,7,5,6,4,8,2
Suma wszystkich sum to 11×10. Ponieważ dwie sumy obok dziesiątki będą większe lub równe 11 nie ma możliwości, żeby na łożysku występowały tylko one. Dla trzech sum rozwiązanie może być następujące: 10, 2, 9, 3, 8, 4, 7, 5, 6, 1.
Domyślam się, że nie jest to jedyne rozwiązanie…
10 tworzy dwie pary o sumach > 10, natomiast 1 utworzy dwie pary o sumach < 12. Z tego wynika, że musimy mieć co najmniej trzy różne sumy.
Spróbujmy dla trzech:
10, 1, 9, 2, 8, 3, 7, 4, 6, 5, 10
Sumy: 10, 11, 15
Minimalna ilość różnych sum wynosi 3. Rozwiązań jest dużo.
Przykładowe rozwiązanie
10 2 8 4 6 5 7 3 9 1
Sumami są liczby 10,11,12.
Jakoś nie chwytam, gdzie tu jest haczyk.
Najprostsze wydaje się ułożenie na przemian duża-mała-duża… na przemian w lewo i w prawo, czyli obok 10 powinny być 1 i 2, potem obok 1 – 9, a obok 2 – 8, potem obok 9 – 3, a z drugiej strony obok 8 – 4 i potem obok 3 – 6, a z drugiej strony obok 4 – 7. A między 6 i 7 powinna być 5.
Czyli wyszło mi, że najmniej mogą być 3 różne sumy sąsiednich kulek: 10,11 i 12, które będą z ułożenia:
-10-1-9-3-7-5-6-4-8-2-
Mniej niż 3 różne sumy chyba się nie da?… Dałabym na przemian sumę 11 i sumę 10, a do tego jedną sumę 15.
10-1-9-2-8-3-7-4-6-5
Rozwiązań dla 3 sum jest więcej, np.:
11, 12, 7
10-2-9-3-8-4-7-5-6-1
11, 13, 4
10-3-8-5-6-7-4-9-2-1
11, 9, 19
10-1-8-3-6-5-4-7-2-9
Nie da się przy różnych liczbach w poszczególnych polach uzyskać ustawienia w którym wszystkie sumy są równe lub takiego w którym wszystkie sumy są równe jednej z dwóch liczb. Czyli najmniejsza możliwa liczba różnych sum to 3. można ją uzyskać np. dla takich ustawień:
10, 1, 9, 2, 8, 3, 7, 4, 6, 5, 10
lub
10, 2, 9, 3, 8, 4, 7, 5, 6, 1, 10
Różnych sum nie może być mniej niż 3, bo sumę=11 daje 5 par wzajemnie rozłącznych, sumę=10 lub 12 dają cztery pary. Mamy więc dla 2 sum co najwyżej 9 par. Musimy więc wziąć jeszcze jedną sumę. Razem 3 różne sumy. A to jeden z możliwych układów dających 3 różne sumy:10, 1, 9, 2, 8, 3, 7, 4, 6, 5.
Moje pierwsze rozwiązanie powstaje poprzez „przeplecenie” tych dwóch ciągów:
1_3_5_7_9
_8_6_4_2_
Do tego „10” na początku lub końcu.
Wydawało mi się, że ten układ pojawi się najczęściej wśród odpowiedzi.
Moje rozwiązanie gdzieś się zapodziało, przysiągłbym, że wysłałem… Znalazłem jedno rozwiązanie „na 3” i tym się zadowoliłem, tok rozumowania był taki, żeby dać 5 par po 11 i potem gdzie się da sumę 7. Czyli 10, 1, 6, 5, 2, 9… tutaj dowolność, a więc 8, i dalej 3, 4, 7, i okazuje się, że jeszcze tylko jedna suma się pojawia, czyli 17. Dowód, że nie da się mieć tylko dwóch sum, mam taki jak u innych rozwiązujących.