Y-2 vel K-2
Następujące zadanie było jednym z najprostszych w finale tegorocznych XIX Mistrzostw Polski w Łamigłówkach:
Umieść w każdym pustym polu diagramu kółko lub krzyżyk. Wszystkie kratki z kółkami powinny tworzyć jeden spójny obszar (wielokąt) i kratki z krzyżykami również. Pola z czterema jednakowymi znakami nigdzie nie mogą tworzyć kwadratu 2×2.
Pozwoliłem sobie zmienić nieco formę – tekst zadania i diagram – zachowując oczywiście to, co merytorycznie istotne. Zastąpiłem po prostu krzyżykami występujące w oryginale czarne kółka, ponieważ tak jest poręczniej dla rozwiązującego, choć przyznaję, że z czarnymi i jasnymi kółkami diagram wygląda ładniej. Mam zresztą do tego typu zadania pewien sentyment, bo pamiętam jego narodziny (rok 1994, japoński magazyn Puzzler). Później zamieszczałem je tu i ówdzie jako otello. Jego japońska nazwa jest przydługa (czarne kółka, białe kółka), a poza Japonią pojawia się zwykle jako yin yang. Wersję z Krzyżykami i Kółkami ochrzciłem mianem K-2 (tak będzie w szykowanym zimowym Omnibusie); jako Yin Yang byłoby Y-2.
Logika K-2 jest prosta i przyjemna. Zadanie z mistrzostw rozwiązuje się, jak mówi moja znajoma pani matematyk, o tak: pyk, pyk, pyk… Podstawowe i w gruncie rzeczy jedyne sposoby są dwa – trzeba stawiać znaki, „uciekając” przed ich odizolowaniem lub przed kwadratem 2×2. Jednak nie zawsze bywa prosto – nawet gdy diagram jest mały i mimo że dwa wspomniane sposoby wystarczają. Z góry gratuluję wszystkim, którzy poradzą sobie z poniższym dość twardym orzechem, choć sprytny początek właściwie załatwia sprawę. Wystarczy podać liczbę wszystkich kółek w rozwiązaniu.
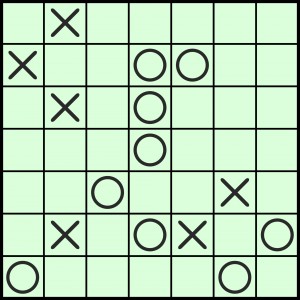
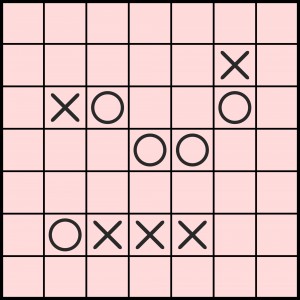

Komentarze
Kółek jest 28.
OOOOOOO
OXXXXXO
OOOXOOO
OXXXXXO
OXOOOXO
OXOXOXO
OOOXXXX
Kółek jest 28. Rozwiązanie wygląda tak (poprzednie to kac powyborczy).
OOOOOOO
OXXXXXO
OXOXOOO
XXOOOXO
XOOXOXO
XOXXXXO
XXXOOOO
Wystarczyły 4 minuty na pozbycie się kaca, czyli nie jest tak źle 🙂
mp
28:
OOOOOOO
OHHHHHO
OHOHOOO
HHOOOHO
HOOHOHO
HOHHHHO
HHHOOOO
Kluczem do rozwiązania są kolejne dwa spostrzeżenia:
– (A) w żadnym kwadracie 2×2 nie mogą występować sytuacje:
ox
xo
ani
xo
ox
– (B) jesli w dwóch punktach brzegu znajdują się takie same znaki to cały brzeg pomiędzy tymi znaczkami z jednej lub drugiej strony musi być wypełniony tym znakiem.
Rozwiązanie:
1. Gdyby w centralnym polu na samym dole był krzyżyk, to obok muszą się znaleźć kółka (zasada niejednorodnego kwadratu). Wtedy z (B) cały brzeg (poza jednym postawionym już krzyżykiem) musi być kółkami – sprzeczność, bo w lewym dolnym rogu powstaje jednorodny kwadrat.
Zatem na samym dole w centralnym polu jest kółko
2. Drugie kółko na brzegu musi być w rogu po prawej u góry
3. Z kolei w lewym dolnym rogu musi być na brzegu jeden krzyżyk…
To oznacza, że cały brzeg po prawej i na prawej stronie dołu jest wypełniony kółkami.
Dalej wystarczy minutka: pyk, pyk, pyk… 🙂
1111111
1222221
1212111
2211121
2112121
2122221
2221111
ooooooo
oxxxxxo
oxoxooo
xxoooxo
xooxoxo
xoxxxxo
xxxoooo
Orzeszek mięciutki:
http://s23.postimg.org/j25wkumff/y2_k2.jpg
1111111
1000001
1110101
1010111
1000010
1110110
0000000
czyli 23 kółka
Nie o to zadanie chodziło.
mp
Każdemu może się zdarzyć 🙂
No a orzech jest rzeczywiście twardy… :/
28 kółek, poszło w miarę gładko, chyba miałem szczęście 🙂
ooooooo
oxxxxxo
oxoxooo
xxoooxo
xooxoxo
xoxxxxo
xxxoooo
czyli 28 kółek
28 czas ok. 30s (bez liczenia kółek) – pyk, pyk,pyk…Panie Marku, podstawowe dwa sposoby nie są wystarczające, by mówić o ROZGRYZIENIU sposobów rozwiązywania tej łamigłówki. A takie całkowite rozgryzienie to bardzo przyjemna i dająca satysfakcję rzecz. Bardzo się przydaje i ułatwia sprawę wiedza jak musi wyglądać zewnętrzna warstwa, czyli pierwszy i ostatni rząd i kolumna (w znaczeniu jak kólka i krzyżyki mogą się tam zachowywać) w związku z założeniem o spójności obszarów. Z tego samego założenia wynika bardzo przydatna zależność jak wygląda czwarty znak w kwadracie 2 na 2, jeżeli mamy po przekątnej dwa takie same znaki a trzeci jest inny. Trzecie wreszcie, warto zauważyć że w każdym rogu 2 na 2 muszą być oba znaki – to właściwie przydatne do szybszego znalezienia drogi rozwiązania. Zresztą rogi są z reguły dobrym miejscem do przyglądania się nie tylko w tej łamigłówce.
Podejrzewam, ze nasi mistrzowie (Przemek i Tomek co roku są na mistrzostwach świata wyżej – szkoda tylko, ze mistrza Polski nie było w tym roku w Bułgarii) zmieścili by się w 20s. Zapraszam w styczniu na strony Sfinksa na eliminacje jubileuszowych XX mistrzostw
Jeśli sposoby konkretyzować (jeżeli …, to …), wówczas rzeczywiście jest ich więcej (naliczyłem 4). Między innymi dlatego ta łamigłówka była w Japonii krytykowana, bo większość zadań (ale jednak nie każde) można rozwiązać „pykaniem” nawet po krótkim praktykowaniu – jak w Pańskim przypadku.
Dzięki za zaproszenie.
mp
PS Bezmyślne postawienie sprintem 34 znaków zajmuje 17 sekund. Pozostaje ok. 13 sekund na myślenie. No, no…
Jest 28 kółek 🙂
A tu obrazek: https://app.box.com/s/lcc20erwmbdabb0eu7dz83zb23jxt5jx
Pozdrawiam
Udało mi się rozwiązać dopiero wykorzystując wielokrotnie informację, że każde rozwiązanie ma tyle samo kółek (istnienie dokładnie jednego rozwiązania też spełnia ten warunek) – a więc np. w tym miejscu trzeba postawić krzyżyk, bo jeśli postawi się kółko to w gotowym rozwiązaniu będzie można zmienić kółko na krzyżyk.
Jestem ciekawy, czy zadanie da się sensownie (tzn. na logikę) rozwiązać nie korzystając z takiej informacji.
Nie rozumiem, co znaczy „każde rozwiązanie ma tyle samo kółek”. Skąd „każde” skoro jest jedno?
mp