Stary rok
Do końca roku zostało jeszcze sporo czasu, więc zadanie z tegoroczną liczbą jest całkiem na miejscu. Oto dwa występy tej liczby w roli mnożnej:
Działania są osobliwe, choć ich niezwykłość niełatwo zauważyć: mnożnik i iloczyn w każdym składają się z dziesięciu różnych cyfr.
Zadanie polega na znalezieniu mnożenia, w którym 2015 będzie mnożną, a mnożnik i iloczyn będą się składały z dziewięciu różnych cyfr – wszystkich oprócz zera. Ściślej, chodzi nie tyle o znalezienie, co o szukanie, a konkretnie o odpowiedź na pytanie: ile co najwyżej mnożeń należy wykonać, aby dotrzeć do rozwiązania?
To rodzaj zadania, które w pierwszej chwili wydaje się katorżnicze do rozwiązywania na piechotę. Do sprawdzenia jest kilkaset mnożników, więc kusi, aby skorzystać z programu. Tymczasem na logikę liczbę możliwych mnożników można znacznie ograniczyć (do ilu?) i korzystając z kalkulatora dotrzeć zaskakująco szybko do (jedynego?) rozwiązania (jakiego?).
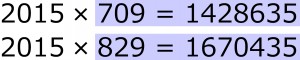

Komentarze
Spodziewałam się zadania o Chopinie 🙂
(???)
SZOPEN+GEORGE=ROMANS 🙂
mp
2015 x 319 = 642785
2015×319=642785
Mnożnik musi być trzycyfrowy (abc), iloczyn sześciocyfrowy.
a=1,2,3 albo 4.
c=1,3,7 albo 9.
2015*319=642785
a jak szukalibyśmy iloczynu bez „9” byłoby:
2015*83=167245
😉
Co do szukania mnożników w zadaniu:
muszą być trzycyfrowe
ale nie mogą być parzyste, bo na końcu będzie 0
liczby mają się nie powtarzać, więc odpada też z mnożnika 5
razem cyfr w mnożniku i wyniku ma być 9, więc największy możliwy mnożnik to 493, bo już dla 497 wynik jest siedmiocyfrowy
i do sprawdzenia zostały 83 mnożniki, ale tylko 1 daje rozwiązanie
Maksymalnie 28 działań, ale już pietnaste daje szukany wynik 2015 * 319 = 642785
Myślę, że ilu rozwiązujących, tyle będzie sposobów 🙂 Trzeba uwzględnić liczby różnocyfrowe, między 100 i 496, bez 0 i 5, bo wiadomo, że wynik będzie się na 5 kończyć, nieparzyste. Nie mogą też kończyć się na 7, bo wynik wtedy kończy się na 05 lub 55. Nie mogą zaczynać się na 12, bo pierwszą cyfrą wyniku jest 2, tak więc pierwszą potencjalną złowioną liczbą jest 139, ale nie pasuje. 143 i 149 też nie. Od tego momentu wynik zaczyna się od 3, więc ostatnia cyfra 3 odpada, zostaje 9. Ale cyfra dziesiątek musi być nieparzysta, inaczej bowiem wynik kończy się na 39, tak więc do sprawdzenia jest tylko 179 (nie pasuje). Wchodzimy w rejon 200+, zdejmujemy sankcje z 3 na końcu, mamy 213 (nie pasuje) i 219 (też nie). Może być 231 (z liczb zakończonych na 1 odrzucamy te, gdzie liczba dziesiątek jest parzysta, bo wtedy wynik kończy sie na 15, no ale tu jest nieparzysta) oraz 239, ale nie jest. Liczby od 240 do 249 odpadają, bo pierwszą cyfrą wyniku jest 4, a od 250 w górę (do 297) jest nią 5, to też odpada. Z wszystkich podanych wyżej powodów wynika, że następną liczbą do sprawdzenia będzie 319, i to jest bingo, bo mamy wynik 642785. Czyli za 9. razem, wynik jednocyfrowy mnie satysfakcjonuje 🙂
Po 10 minutach przeglądania wszystkich możliwości znalazłem 2015*319=642785.
Wiadomo, że mnożnik musi być w zakresie 123 – 497, musi być liczbą nieparzystą, nie może kończyć się na 5, nie może mieć powtarzających się cyfr…
2015*319=642785
Wydaje mi się, że jest to jedyne rozwiązanie
Ile mnożeń trzeba wykonać trudno powiedzieć. Przedstawie natomiast moje dojście (trochę fartowne) do rozwiązania.
1. Mnożnik i iloczyn muszą mieć łącznie 9 cyfr. Zatem mnożnik musi być w przedziale 123-496.
2. Ostatnią cyfrą mnożnika nie może być cyfra parzystą, gdyż wówczas ostatnią cyfrą iloczynu byłoby zero.
3. Ostatnią cyfrą mnożnika nie może być 5 gdyż w takim przypadku ostatnią cyfrą iloczynu również byłoby 5.
4. Ostatnią cyfrą mnożnika nie może być 7 gdyż iloczyn kończyłby się cyframi 55 lub 05.
5. Teraz istotna rzecz. Ostatnią cyfrą wyniku na pewno będzie 5 więc iloczyn nie może mieć cyfry 5 na żadnym innym miejscu w szczególności jako pierwszą cyfrę.
6. Daje nam to wyeliminowanie części możliwości utworzenia mnożnika. Konkretnie przedział z pkt1 zostanie ograniczony do dwóch przedziałów: 123-243 oraz 298-489.
7. Następnie próbowałem ograniczyć skrajne wartości przedziałów. Z pierwszym przedziałem na pierwszy rzut oka wszystko jest ok. Drugi przedział natomiast jako dolne ograniczenie ma cyfrę parzystą na końcu, więc należy je nieco zwiększyć. 299 odpada z uwagi na dwie dziewiątki. 300-310 odpada z uwagi na zero. 311 z uwagi na dwie jedynki, 312, 314, 316, 318 z uwagi na cyfrę parzysta na końcu. 313 z powodu dwóch trójek. 315 i 317 z uwagi na 5 i 7 na końcu. 319 pasuje. Pomnożyłem i voilà – miałem farta.
Chmmm… Nie miałem zbyt wiele czasu na myślenie o zadaniu. W sumie to myślałem tylko podczas jazdy rowerem, więc bez kartki, bez ołówka oraz przy pełnej koncentracji na sytuacji w ruchu drogowym.
Ale nie nasuwają mi się żadne pomysły jak ograniczyć liczbę „dobrych” mnożników.
Nawet znając rozwiązanie (bo komputer oczywiście znalazł w mgnieniu oka), nie mam pomysłów…
No ale mamy piątek, weekend przed nami, więc może nadarzy się okazja do zdobycia kartki i ołówka… Życzę miłego weekendu autorowi bloga oraz czytelnikom 🙂
PS. Tak przy okazji: ostatnio wpadło mi w garść ciekawe zadanie z monetami, ważeniem itp…
Mamy 100 monet, wszystkie wyglądają identycznie. 30 z nich jest prawdziwych i każda z nich ma identyczną masę. Pozostałe są fałszywe i wiemy o nich dwie rzeczy:
– każda z monet fałszywych jest cięższa od monety prawdziwej
– każde dwie monety fałszywe mają różne masy.
Pytanie: Jaka jest minimalna liczba ważeń, które musimy wykonać, aby znaleźć przynajmniej jedną monetę prawdziwą?
Ja na razie znalazłem rozwiązanie z 70 ważeniami (podczas jazdy rowerem 🙂 ), ale podejrzewam, że da się o wiele lepiej 🙂
Ja nie wykonałam jakiejś specjalnej analizy… Wymyśliłam tyle, że mnożna musi być nieparzysta, 3-cyfrowa i mniejsza od 490, a wynik musi być 6-cyfrowy. Pomyślałam, że sprawdzę kilka liczb na kalkulatorze i zobaczę, czy jeszcze jakaś cecha mi się nasunie. Na (nie)szczęście zaczęłam od 300 w górę. Znalazłam więc właściwą liczbę po paru próbach i zadanie się dla mnie skończyło, zanim się na dobre zaczęło.
Dziękuję za kryptarytm ;), ale nie dam rady rozwiązać go na piechotę… A użycie programu to żadna frajda.
Kryptarytm ułożył się naprędce i rzeczywiście – wygląda na siermiężny, czyli b. ciężki do ruszenia na piechotę.
mp
Chciałbym tylko skomentować, że istnieje coś pośredniego między liczeniem „na piechotę”, czy na kalkulatorze, a programowaniem, mianowicie wykorzystanie arkusza kalkulacyjnego, konkretnie excela. Tam właśnie można najszybciej „zobaczyć” np., że jeśli dana liczba kończy się na pewną cyfrę, to determinuje to dwie ostatnie cyfry wyniku, i w konsekwencji na przykład odrzucenie ostatniej cyfry 7 i połowy liczb kończących się na 1. Już nie mówię oczywiście o szybkim rozwiązaniu, ale jak rozumiem sens zadania polegał nie tyle na jego znalezieniu, ile właśnie na sposobie. Z samym kalkulatorem pewnie zajęłoby mi to więcej czasu, przyznaję.
A ja przyznaję (się), że o ile programowanie nie jest mi obce, to o arkuszu kalkulacyjnym nie mam zielonego pojęcia, choć przy różnych okazjach (jak powyższy komentarz) nachodzi mnie ochota, aby się weń wgryźć.
mp