Piramida XYZ
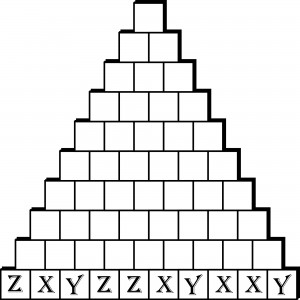
W podstawie piramidy jest 10 bloków. W każdy wpisujemy jedną z liter X, Y, Z – ich układ może być dowolny, na przykład taki jak poniżej.
Zaczynamy wieloetapową operację: w każdym etapie wpisujemy do kolejnego rzędu bloków litery X, Y, Z zgodnie z dwiema zasadami:
– jeśli wyższy blok styka się z dwoma blokami, w których są różne litery, to wpisujemy doń trzecią (inną niż te dwie) literę;
– jeśli wyższy blok styka się z dwoma blokami, w których są takie same litery, to wpisujemy doń taką samą literę jak te dwie.
Po dotarciu do szczytu piramidy rozmieszczenie liter będzie następujące:
Piszemy o tym, co ważne i ciekawe
Diabeł i raj Katarzyny Gärtner
83-letnia dziś Katarzyna Gärtner, słynna kompozytorka „Małgośki” i wielu innych przebojów, tuła się po domach przyjaciół i stara odzyskać dom, studio oraz swój dorobek artystyczny.
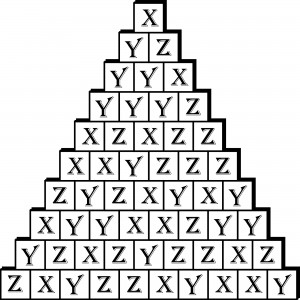
Jeżeli w tej piramidzie taką operację wykonalibyśmy wielokrotnie, to okazałoby się, że:
w trzech narożnych blokach – dwu skrajnych w podstawie oraz w szczytowym – litery zawsze są albo wszystkie takie same albo wszystkie różne – niezależnie od początkowego układu liter w podstawie.
Pytania są dwa:
Gdybyśmy mieli trzy znacznie większe, wręcz kosmiczne piramidy, to w przypadku której z nich powyższa zasada (wyróżniona kursywą) byłaby zachowana – z liczbą bloków w podstawie, której końcówką byłoby …001, …002 czy …003?
Dla jakiej liczby bloków w podstawie (wzór ogólny) spełniona jest ta zasada?

Komentarze
W tej piramidzie łatwo znaleźć ‚podpiramidy’, w których zasada nie jest spełniona:
na przykład w rogach piramidy o podstawie 5 jest ZZX… lewy dolny róg. Można znaleźc kilka innych piramid mniejszego kalibru.
Wzór ogólny: liczba kratek w dolnym rzędzie piramidy musi po odjęciu 3 lub odjęciu 4 być podzielna przez 6. A zatem ani 001, ani 002, ani 003 niczego nie gwarantują. Potrzebna jest suma cyfr całej liczby.
Wstępne badania wykazują, że wystarczy w podstawie mieć parzystą liczbę bloków i wtedy wszystkie trzy wierzchołki piramidy będą spełniać regułę rządzącą jej ‚wzrostem’.
…jednak nie… zaczyna mi tu kombinatoryką pachnieć…
By wspomniana zasada była zachowana ilość bloków w podstawie musi wynosić x*5 +4 gdzie x to kolejne liczby naturalne. Warunek nie będzie spełniony dla żadnej z wymienionych końcówek. Na pewno każda liczba z końcówką ..004 będzie spełniała podany warunek.
Pierwsze pytanie jest proste to musi być 002. Bo musi być parzysta podstawa, dla każdej nieparzystej podstawy większej niż jeden możemy ustawić alternatywnie XYXYXYXYXYX.
I w dolnych rogach podstawy będziemy mieć X X a powyżej już w całej piramidzie same Z.
Nad wzorem ogólnym pracuję
P.
Poproszę o wyjaśnienie, bo chyba nie rozumiem zadania. Jeśli początkowy układ liter będzie np. X Y Z Z Z Z Z Z Z Z, to oczywistym jest, że zasada kursywą napisana nie będzie spełniona. A w zadaniu jest napisane, że jest spełniona dla wszystkich początkowych układów liter…
*********Y
********Y Y
*******Z X Z
******X Y Z Z
*****X X Z Z Z
****Z Y Z Z Z Z
***Y X Z Z Z Z Z
**Y Y Z Z Z Z Z Z
*Z X Z Z Z Z Z Z Z
X Y Z Z Z Z Z Z Z Z
Czyli zasada jest spełniona. Czy ten przykład rozwiewa niejasności?
mp
Ja tu widzę trójkąt Pascala
Zamieniłem literki na cyferki 0, 1, 2, a zasadę doboru trzeciej wartości na taką: nad dwiema kratkami z liczbami a i b będzie liczba (-a-b) mod 3.
Nad a, b, c będzie (a+2b+c) mod 3.
Nad a, b, c, d będzie (-a-3b-3c-d) mod 3.
Itd.
Jeśli liczba przy literce będzie podzielna przez 3, to wyraz można wyrzucić z nawiasu. Celem jest wyrzucenie wszystkich wyrazów poza skrajnymi. W ten sposób (-a-3b-3c-d) mod 3 przekształca się do (-a-d) mod 3, co jest dziwnie podobne do (-a-b) mod 3.
Zasada będzie spełniona, gdy wiersz trójkąta Pascala będzie zawierał same liczby podzielne przez 3 (za wyjątkiem skrajnych jedynek). A to, zdaje się, będzie spełnione dla trójkąta o boku równym potędze 3 (długość boku liczymy, jako liczbę kratek minus jeden).
Czyli trójkąty z liczbą kratek w podstawie: 2, 4, 10, 28, 82… Bonusowo oczywiście 1.
Dowodził nie będę, bo nie potrafię.
Ale mogę pokazać rysunki: http://www.discreteteaching.com/documents/pascaler/PascalTalk.pdf (strona 14)
Brawo! To pierwsze i jak dotąd jedyne poprawne rozwiązanie.
mp
Jeszcze odpowiem na pierwsze pytanie: kosmiczne potęgi 3 w pewnym momencie osiągają …001. Do tego musimy dodać 1, więc odpowiedzią jest …002.
Nigdy potęga nie będzie miała końcówki …000, ani …002.
wzór ogólny powinien uwzględniać piramidkę o podstawie 2
Piramidka nie może mieć nieparzystej liczby boków, czyli wybieram …002
tak na oko 82 jest OK. 82 = 1 + 9*9.
Czyli kolejna piramidka to 1 + 81*81 i ogólnie
a_1 = 2
a_2 = 10
a_n = 1 + (a_{n-1})^2
ale to nie muszą być wszystkie rozwiązania, zwłaszcza że przejście z 2 do 10 jest w tym wzorze sztuczne
2,4,10,16,…, 4+6k,…
@cpp i @Brzeszczot: może połączyć te 2 wzory?
2k+2, czyli 002 jest gwarantem.
002 – tak, wzór – nie.
mp
Ogólnie rzecz biorą zasada będzie spełniona gdy liczba bloków w podstawie wyraża się wzorem n = 3^k + 1
Początkowe wartości to: 2, 4, 10, 28, 82, 244, 730, …
A teraz uzasadnienie (nie do końca formalne, raczej jego idea):
Litery X, Y, Z zastępujemy liczbami 0, 1, 2. Od tej pory wszystkie operacje wykonujemy z ciele Z3, czyli modulo 3, tzn. zawsze jako wynik przyjmujemy resztę z dzielenia otrzymanej liczby przez 3.
Zasada wypełniania tabeli mówi, że jeśli mamy dwie sąsiednie komórki o wartościach a oraz b, to komórka znajdująca się bezpośrednio nad nimi (c) przyjmuje wartość 2a+2b (proszę sprawdzić dokładnie, że jest to prawda).
Zacznijmy wypełniać tabelę od góry, przy czym tym razem w komórki będziemy wpisywać liczbę, która mówi, z jaką krotnością dana komórka wlicza się do wartości na samym szczycie (nazwijmy ją ostatecznym wynikiem).
Oczywiście wartość na samym szczycie wlicza się do ostatecznego wyniku jeden raz, zatem na górze mamy wiersz:
1.
Wartości z poniższego wiersza wliczają się podwójnie, zatem kolejny wiersz, to:
2, 2
W kolejnym wierszu komórki skrajne wliczają się podwójnie na każde wystąpienie wartości w drugim wierszu (czyli 2*2 = 4 razy), natomiast środkowa wartość wlicza się 2 razy na każdy składnik powyżej, zatem wychodzi 2 * (2 + 2) = 8 razy. Zatem trzeci wiersz to:
4, 8, 4
Kolejne wiersze wyglądają tak:
8, 24, 24, 8
16, 64, 96, 64, 16,
32, 160, 320, 320, 160, 32
…
Teraz zauważmy, że jeśli wiersze ponumerujemy od góry począwszy od 0, oraz w k-tym wierszu wszystkie liczby podzielimy przez 2^k, to otrzymamy zwykły trójkąt Pascala!
Teraz trzeba sobie zadać pytanie, kiedy liczby występujące wewnątrz dolnego wiersza pewnego trójkąta nie mają wpływu na ostateczny wynik? Jest tak tylko wtedy, gdy w danym wierszu występują tylko liczby podzielne przez 3 (oczywiście poza lewym i prawym skrajem wiersza).
Ponieważ mnożenie wartości w wierszach przez 2^k nie wpływa na podzielność przez 3, zatem właściwe pytanie brzmi: w których wierszach trójkąta Pascala występują tylko i wyłącznie liczby podzielne przez 3 (oczywiście poza brzegami).
Teoria liczb mówi nam, że jest tak tylko dla wierszy o numerz będącym potęgą liczby 3.
Jeszcze raz podkreślam, że powyższe to tylko konspekt rozwiązania/uzasadnienia, mam nadzieję, że czytelnicy zrozumieją ideę opisu i będą potrafili uzupełnić szczegóły
To jeszcze odpowiadając na pierwsze pytanie:
Skoro liczba bloków w dolnej podstawie ma mieć postać 3^k + 1, to tylko końcówka …002 wchodzi w grę.
Najmniejszą (*) taką liczbą jest 3^100 + 1, a ogólnie są to liczby postaci 3^(100k) + 1.
(*) Jeśli uwzględnimy, że n = 3^0 + 1 = 2 kończy się cyframi …002, to n = 2 też jest dobre
2, 4 10, 28, 82, 244, 730, 2188,…….czyli:
f(1)=2
f(n)=3*f(n-1)-2
tylko jeszcze nie widzę z czego to wynika
Chyba jednak tego zadania (wzór ogólny) nie da się rozwiązać w głowie…
Z tym Kominiarzem to jest wpadka


Zalogowałem się u znajomego a mimo to wskoczyły jego dane czego nie zauważyłem. Dla sprawdzenia, zalogowałem się po raz drugi, uważając co się dzieje, lecz system i tak znów wrzucił jego dane. Coś jest nie tak z tym logowaniem:/
Najpierw doświadczalnie wyznaczyłem wzór ogólny na liczbę bloków w podstawie piramidy, dla której spełniona jest zasada:
3^n+1
Szkoda, że nie umiem tego udowodnić
Z pomocą „wujka Wolframa” znalazłem odpowiedź na pierwsze pytanie.
Ponieważ 3^n modulo 1000 może wynosić 1 ale nie 0 lub 2, więc liczba bloków w podstawie kosmicznej piramidy może mieć tylko końcówkę …002
3^n + 1, n = 0,1,…
czyli
2,4,10,28,…
To może dodajmy kolejny problem: jak duża jest najmniejsza piramida, spełniająca warunki zadania, mająca w zapisie dziesiętnym postać …001, …002 lub 003?
Odpowiedź na dodatkowe pytanie zadane przez cpp:
3^100+1
@cpp
f(1)=2, f(n)=3*f(n-1)-2
f(101)=…002
f(102)=…004
Pieszo-monotonne. Czy zadanie można rozwikłać w oparciu o podpiramidy z piramidy<100 bloków w podstawie?
…i tak:
f(101)=515377520732011331036461129765621272702107522002
i ma 48 cyfr,
f(102)=1546132562196033993109383389296863818106322566004
i ma 49 cyfr
Te liczby kończą się tylko na 0,8,2,4 więc o końcówkach …001 ani …003 nie ma mowy.
to jeszcze dodam, jak znalazłem swoje rozwiązanie.
Oczywiście zaczynamy od podstawienia x,y,z=0,1,2.
Potem widzimy, że w każdej (pod)piramidce o podstawie 2 suma liczb dzieli się przez 3. Potem zaczynamy od dołu i kombinujemy, jak duża musi być piramida, aby wartość w górnym wierzchołku zależała tylko od wartości w narożnikach na dole. Możemy wziąć dowolną konfigurację na dole i zaburzyć ją np. o +1 (mod 3). Ze względu na właściwość piramidek o podstawie 2, zaburzenie to przeniesie się do górnego rzędu jako ….-1, -1,… To z kolei w kolejnym wierszu da …,+1,-1,+1,… i dalej ..-1,0,0,0-1. Ha! zaburzenie w wierszu N przechodzi do N-3 tylko na 2 polach. Następny taki przypadek to N-9 (zaburzenie w wierszu N przechodzi do N-9 na maksymalne 2 polach).
Potem trzeba zauważyć, że brzegi piramidki nie wnoszą niczego do zaburzenia – co najwyżej ono wychodzi poza piramidkę i wtedy znika.
Stąd szybko można wyprowadzić, że zaburzenie w ostatnim wierszu przenosi się na tylko 2 pola wiersza N-K dla K = 1,3,9,27,… stąd teza. Dla podstawy piramidy o podstawie 1+3^n wartość górnego wierzchołka zależy TYLKO od dolnych, przy czym zaburzenie dolnego o +1 powoduje zmianę wartości górnego o -1 (mod 3).