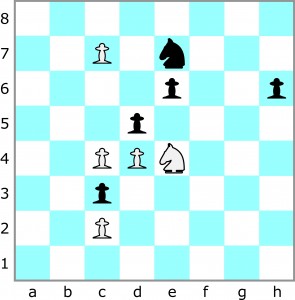
Czterochodówka
Zaczynają białe i wygrywają w czterech ruchach.
Wypada jednak wyjaśnić, co jest grane, bo przecież nie szachy, skoro na planszy panuje bezkrólewie.
Otóż jest to końcówka partii młynka szachowego. Gracze wykonują ruchy na przemian: skoczkiem – dokładnie tak, jak w szachach, pionkiem – tak, jak królem szachowym, czyli o jedno pole w dowolnym kierunku na wprost lub na ukos. Nie ma bicia. Celem gry dla każdej ze stron jest ustawienie dowolnych czterech swoich bierek w linii prostej na czterech kolejnych polach – w wierszu, w kolumnie lub wzdłuż przekątnych. A zatem – do dzieła!

Komentarze
c2-b3 c3-b4
Sc5 b4-c3
b4
i „mat ” skoczkiem na a4 lub e4
Białe wykonują jako pierwszy ruch 2b3, czym zmuszają czarne do b4. Białe wykonują Sc5. Rozważmy dwie możliwości: czarne wracają na c3, wtedy biały pion dochodzi z b3 na b4 i bez względu na ruch czarnych, skoczek może skoczyć na (a4 lub e4) kończąc grę. Druga możliwość – czarne nie wracają na c3. Wtedy białe wykonują dc3 i, czarne nie mogą im już w tym przeszkodzić, bc2. Czym także kończą rozgrywkę.
drugie rozwiązanie
c2-d3 e6-e5 (groźba mata na f4)
d3-e3 e5 – f4 (skoczek na f4 też nie pomaga)
c4-c5 czarne: cokolwiek
Sf2 lub c7-b6 mat
Ile jest różnych rozwiązań?
Moim zdaniem (niestety) dwa – tzn. dwa różne pierwsze ruchy białych.
mp
c7-d6 wydaje się prowadzić do „mata” w 3 posunięciach
(grozi dojściem tym pionkiem na b4 lub f4, a w przypadku obrony pionem c3 białe dają „mata” na c3).
Olśniło mnie. Zadanie nie ma rozwiązania.
??? o_O
mp
Wielkie pytające oczy? Tego się nie spodziewałem.
Czekam na pierwsze posunięcie białych.
c2-b3
mp
We wstępie wpisu mamy polecenie:
„Zaczynają białe i wygrywają w czterech ruchach”, czyli, nie chodzi o to, aby białe wygrały w np. jednym, dwóch, trzech, pięciu, itd. ruchach, ale właśnie dokładnie w czterech posunięciach.
Rola bierek czarnych sprowadza się do uniemożliwienia zamiaru białych, czyli, niedopuszczenia do sytuacji, w której białe w swoim czwartym posunięciu ustawią cztery swoje bierki w linii prostej na czterech kolejnych polach. Jeśli np. białe „wygrają” grę po dwóch posunięciach, to w sensie żądania z wpisu „przegrają”, bo nie wygrały w czterech posunięciach.
c2-b3, d5-c5
Panie Andrzeju, podążając Pana tokiem myślenia: czy uważa Pan, że czarne mogą zmusić białe do wygrania w mniej niż czterech ruchach?
mp
Czarne białych do niczego nie zmuszają, to białe chcą wymusić na czarnych taką grę jaka im odpowiada. Bez współpracy czarnych białe nie osiągną swojego celu jakim jest wygrana w czterech ruchach.
Przykład.
Po c2-b3 białe żądają, aby czarne zagrały c3-b4. Czarne odmawiają (nie są samobójcami) współpracy z białymi i grają np. h6-g6 z nieuchronnym zakończeniem gry po trzech posunięciach.
Co teraz mogą zrobić białe? Czy mogą zakończyć grę posunięciem b3-b4? Nie mogą, bo ich celem była wygrana w czterech, a nie w dwóch ruchach.
No i wykonują (białe) jakiś trzeci ruch (oczywiście taki, żeby im czarne nie przeszkodziły wygrać w czwartym ruchu), potem ruszają się czarne i białe kończą czwartym ruchem. I wszystko gra 🙂
m
Zgadza się, wszystko gra, ale fałszywie.
Czarne zawsze będą mogły zakończyć grę w trzech ruchach, bez względu na to co zrobią białe. Białe, co najwyżej , w czwartym swoim posunięciu, mogą podpisać kapitulację.
Zadanie nr 3 w „Na pamięć” z 27.09.2014 ma oprócz podanego jeszcze trzy inne rozwiązania. Aby rozwiązanie było jedno należałoby ustawić puste obszary np. tak:
oooooo
oooFFF
FF__Fo
oFFFFo
ooFooo
oFFF_o
oooo_o
oooooo
Zadanie jest OK. Powiększyłem powierzchnię prostokąta zamiast 7×6 użyłem prostokąta 8×6. Przepraszam
c2-d3 d2-c5
d3-e3 cokolwiek
d3-f4
albo czarne nie blokujaąprzekątnej i wtedy
c2-d3 e6-f5
c4-c5 cokolwiek nie powstrzyma ustawienia
d3 na e3 i (c7 na b6 albo e4 na f2)
Urlop? Choroba?
Na szczęście tylko brak czasu
mp
Komentarze ujawniono w niedzielę. Czy będzie zatem nowy wpis?
Społeczeństwo domaga się następnego zadania 🙂
Wybacz społeczeństwo, ale z powodu nawału innych zajęć będzie mała jesienna zapewne parotygodniowa przerwa.
mp
To może chociaż jakieś bardzo hardcorowe zadanie, takie akurat na parę tygodni?
Panie Marku, piniondz jest piniondz, ale proszę nie zawodzić Pańskich fanów i fanów Łamibloga 🙂
Ja się wręcz domagam następnego wpisu! Proszę się nie kłaść spać tylko pitrasić następny wpis!
😀
Na pamięć nr 16 z 11/10/2014r.
Zadanie nr 6 na jeszcze jedno rozwiązanie 450 * 9 =4050.
Tak samo zadanie nr 5
5
19
3 10 2
8 4 6 7
Trafne i fajne uwagi.
mp