Krzyż w kratkę
To dziwne: szósty Omnibus wakacyjny jest w sprzedaży już od trzech tygodni, a ja jeszcze nie dostałem od wnikliwych czytelników żadnego maila, wytykającego mi jakiś błąd. Gdybym wiedział skądinąd, że choć jeden taki błąd popełniłem, brak reakcji czytelników byłby bardzo dziwny. A tak jest tylko dziwny, bo prawdopodobieństwo, że w dość obszernym zbiorku różnego rodzaju zagadek wszystko gra, jest bliskie zera. Wiem jedynie o paru niedoróbkach mniejszej wagi, czyli korektorskich oraz tzw. głupich błędach. Na przykład w quizie na s. 51 w punkcie 19 jest mowa najpierw o tysiącach kilometrów, a potem tylko o 5 i 15 km (km-y są oczywiście niepotrzebne).
Nie znaczy to, że maili z zarzutami w ogóle nie otrzymałem. Było kilka, ale się wybroniłem, choć w jednym przypadku mój oponent może pozostać przy swoim zdaniu. Chodzi o uwagę dotyczącą punktu 10 w Alternatywach ortograficznych na s. 40, czyli o wskazanie, która forma jest poprawna – „Krzyżacy” czy „krzyżacy”. Ogólna zasada mówi, że nazwy zakonów piszemy małą literą (chyba że są to pełne nazwy oficjalne, czyli w przypadku Krzyżaków: Zakon Szpitala Najświętszej Maryi Panny Domu Niemieckiego w Jerozolimie). Jednak „Krzyżacy” są wyjątkiem – duża litera na początku wynika z tradycyjnej formy zapisu, która się przyjęła i uodporniła na regułę. Kłopot z tym, że stawia coraz mniejszy opór i od kilku lat w poważnych publikacjach pojawiają się czasem „krzyżacy”. Moja linia obrony formy „Krzyżacy” sprowadza się do tego, że póki co, o ile mi wiadomo, w żadnym słowniku języka polskiego pisownia małą literą nie jest dopuszczona jako alternatywna, więc pozostaje „buntem na pokładzie”.
Przy okazji krzyżackiego tematu przypomniało mi się zadanie, które opublikowałem naście lat temu na łamach holenderskiego, ale anglojęzycznego pisma Cubism for Fun. Właściwie jest to problem do dziś nie rozwiązany, tzn. nie ma pewności, czy najlepsze znane rozwiązanie jest rzeczywiście najlepszym.
Szachownica złożona z 64 pól może mieć kształt krzyża. Jak rozciąć ten krzyż – tnąc wzdłuż granic między polami – na najmniejszą liczbę części, z których będzie można złożyć typową szachownicę 8×8? Wiadomo, że części nie może być mniej niż 4 (choć dowód, że to minimum, nie jest znany), a prosty podział wygląda na przykład tak:
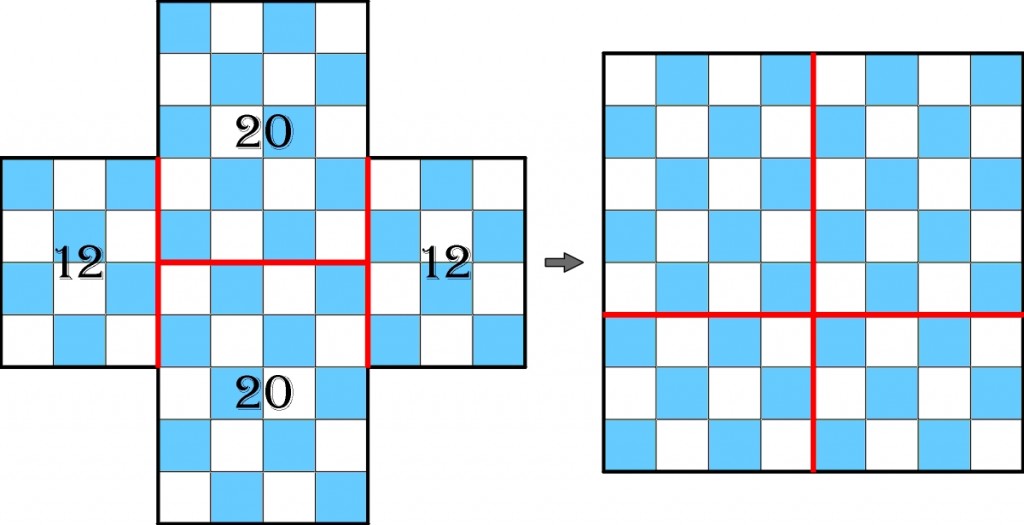
Konkretne zadanie polega na znalezieniu podziału optymalnego, czyli takiego, przy którym iloczyn powierzchni czterech części będzie maksymalny. Określenie „optymalny” bierze się stąd, że ideał stanowi podział na cztery części o jednakowej powierzchni – iloczyn byłby wówczas największy możliwy, równy 16^4, czyli 65536. Niestety, po podzieleniu krzyża na części takiej samej wielkości ułożona z nich szachownica nie będzie… szachownicą, na przykład:
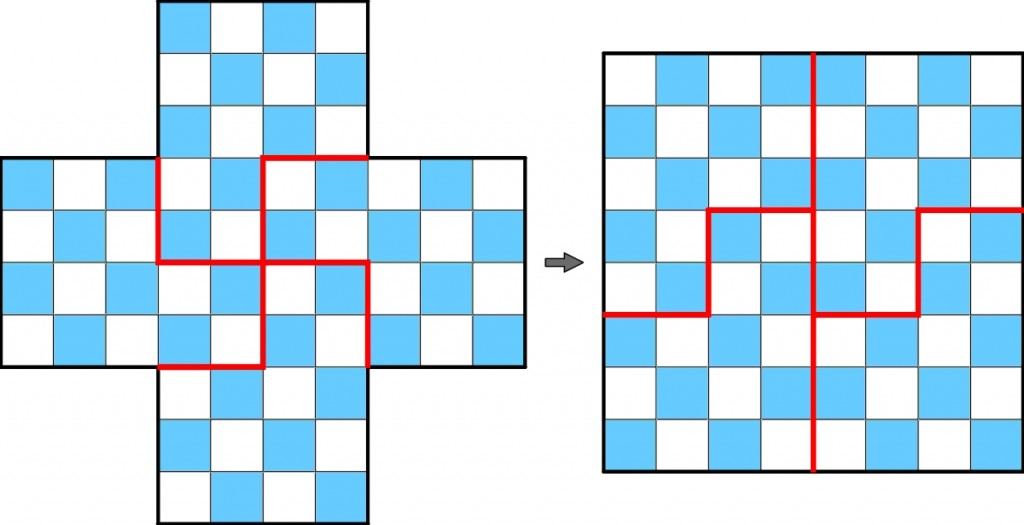
W pokazanym wyżej podziale dwie części mają powierzchnię 12 i dwie 20, więc iloczyn równy jest 57600. Może być jednak lepiej:
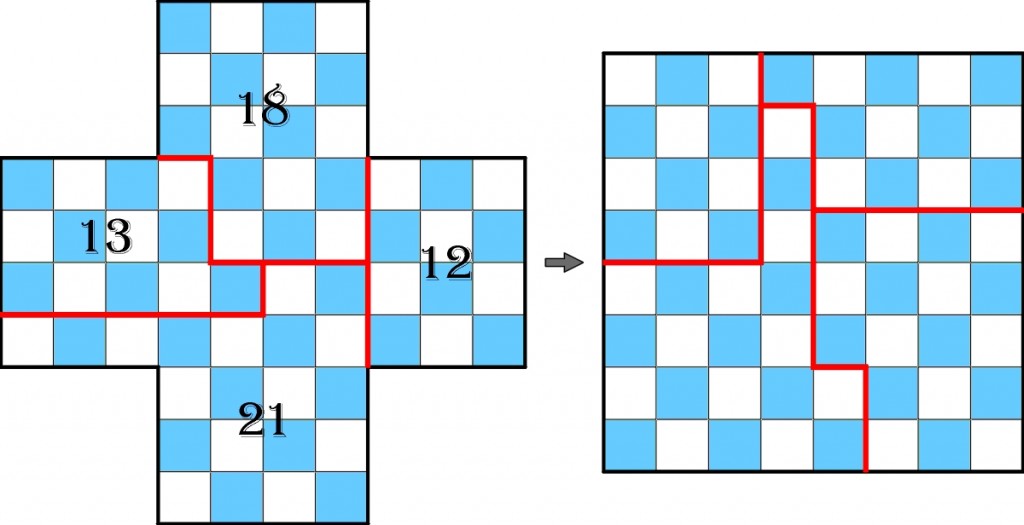
Teraz iloczyn równy jest 12×13×18×21=58968.
Ale może być jeszcze lepiej, czyli z większym iloczynem. Jak i z jakim?
Zadanie stanowi niewątpliwie bardzo twardy orzech, więc jest mała szansa, że ktoś się skusi i spróbuje je chociaż nadgryźć. Ale może…

Komentarze
Piąty (jeden Omnibus był zimowy) „Omnibus wakacyjny” jest dla mnie zagadką. Jak Pan, Panie Marku, i Pana współpracownicy znaleźliście czas i świetne pomysły, aby mogło powstać tak niezwykłe dzieło?
Gratuluję dobrej roboty.
PS Czworaczki (str.12) diagram 1-5
Dziękuję Panie Andrzeju (współpracownicy nie dziękują, bo ich nie ma).
Nie mogę się połapać, o co chodzi z Czworaczkami.
mp
Czworaczki (str.12) diagram 1-5.
Oprócz podanego w Omnibusie rozwiązania jest jeszcze druga odpowiedź:
12345
25413
43521
54132
31254
Konik trojański (str.48) ma dwa rozwiązania, a różnią się one rozmieszczeniem cyfr: 1, 4, 9.
„Omnibus wakacyjny” tak mnie zauroczył, że na razie bardziej go oglądam niż szukam odpowiedzi na zawarte tam zadania. A jak już zaczynam szukać rozwiązań, to robię to z umiarem, aby starczyło rozwiązywania na jak najdłużej.
Mówiąc o współpracownikach trochę się zagalopowałem. Miałem na myśli np. drukarzy, którzy postarali się o to, aby nie zepsuć Pana , Panie Marku, dobrej roboty.
Pozdrawiam i jeszcze raz gratuluję.
No, nareszcie, są jakieś niedoróbki merytoryczne – małe bo małe, ale jednak. Wiedziałem, że mogę na Pana liczyć 😉
To, że Omnibusa przyjemniej się przegląda niż rozwiązuje 😉 jest przede wszystkim zasługą grafika – bez jego talentu i zaangażowania całość straciłaby przynajmniej połowę uroku.
Saluti cordiali
mp
Ja się bardzo chętnie skuszę. Ale pierwsza próba okazała się na tyle satysfakcjonującą, że nie zamierzam podejmować dalszych prób 🙂
12×16×16×20 = 61440
http://i.imgur.com/eUq7zUa.png
Wspaniale! To rekord – wynik lepszy od najlepszego dotychczasowego (59136 = 12*14*16*22). Gratuluję!
mp
Po złamaniu kilku ołówków uzyskałem taki wynik
http://pokazywarka.pl/arx40s/
Rozwiązanie to otrzymałem przekształcając (metodą prób i błędów) najlepszy rezultat podany we wpisie. Do układania kwadratu użyłem programu „PolySolver” Jaapa Scherphuisa.
Rekord wyrównany!
mp
Ja też przyłączam się do gratulacji z powodu kolejnego numeru Omnibusa. Jak też udziału w tym nowym dodatku do Wyborczej, co ktoś wspominał we wpisie do poprzedniego zadania. Co do Omnibusa, to już wcześniej zauważyłem, że w Pana ujęciu „największe państwo”, bądź jakaś inna kraina czy jednostka terytorialna, to coś o największej powierzchni. Ja pamiętam ze szkoły. że skłanialiśmy się do poglądu, iż co najmniej równoprawnie chodzić może, zwłaszcza w przypadku państw, a nie np. wysp, o liczbę mieszkańców. I dlatego np. w pytaniu o największe państwo w Europie nieposiadające dostępu do morza ktoś mógłby odpowiedzieć B jak Białoruś, no ale pod względem liczby mieszkańców to jest C jak Czechy, ok. miliona więcej (a W jak Węgry około pół miliona). To znaczy ja już wiem, co Pan ma na myśli, ale ktoś mniej doświadczony w Pana zagadkach może mieć wątpliwości, dlatego może by dodawać „pod względem powierzchi”, albo czasem użyć słowa np. „najrozleglejszy”… Najlepszy przykład, gdy mówi się o „największych państwach UE”, to Polskę wskazuje się na 6. miejscu, i nikt nie zaprząta sobie głowy np. Szwecją czy Finlandią.
Jeśli chodzi o dodatek do GW, to podobało mi się zadanie o układaniu kwadratu z kropek, których pewna liczba (np. 2) miała leżeć w danej figurze geometrycznej, np. w trójkącie (niestety nie mam w tej chwili tego przed sobą). Oczywiście tak prosto się nie udaje, więc wymyśliłem, że kwadraty to będą również te ustawione w „karo”. Co też nie bardzo wychodziło, no ale uznałem, że podchwytliwość może być w tym, że tam jest też drugi trójkąt, taki mniejszy, powstały w wyniku chyba odcięcia bokiem trójkąta kawałka kwadratu, i to mi wyszło: jedna kropka w tym dużym trójkącie, a druga w tym mniejszym. Zadowolony zaglądam do odpowiedzi… po czym okazuje się, że rozwiązanie jest jeszcze inne i kwadrat jeszcze bardziej wyrafinowany, lub jak kto woli „kopnięty” 🙂 a trójkąt po prostu ten jeden i nie ma co mnożyć bytów ponad potrzebę. Jak to czasami czytelnik jednak nie nadąża za intencjami autora. Co do zadania z szachownicami, to nie wiem, może w weekend, ale chyba jest trudne w sensie dużej liczby przypadków do rozpatrzenia. Pozdrawiam.
Dziękuję.
Jakoś nie chce mi się wierzyć, aby ktoś na pytanie „które państwo jest większe – Kanada czy Polska?” odpowiedział, że Polska albo poprosił o uściślenie, czy chodzi o powierzchnię, czy o ludność. Ale może jestem małej wiary. Co innego w przypadku miast, bo miernikiem wielkości miasta jest tradycyjnie liczba mieszczan:)
mp
A propos miast (Głogów, etc.), to był to największy hit towarzyski na wczasach.