Łaciaty inaczej
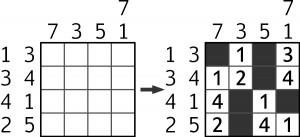
Przykład zadania z kwadratem łacińskim „łaciatym” z 17 kwietnia wyglądał tak:
A ogólne zasady zabawy były następujące:
Do niektórych pól kwadratu n×n należy wpisać cyfry od 1 do n – nie powtarzając tej samej cyfry w żadnym wierszu i kolumnie – a pozostałe pola zaczernić. Kluczem do rozwiązania są liczby przy brzegu diagramu. Każda z nich stanowi sumę kolejnej grupy cyfr w danym rzędzie (grupy mogą być jednocyfrowe).
Kwadraty w łaty można jednak „szyfrować” na wiele innych sposobów, chyba ciekawszych. Na przykład:
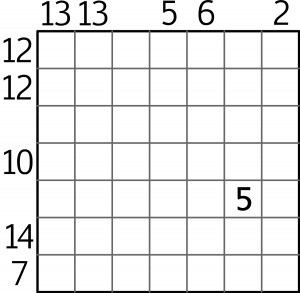
W każdym rzędzie kwadratu n×n powinny się znaleźć cyfry od 1 do n-2 oraz dwa czarne pola. Liczba przy brzegu oznacza sumę cyfr między czarnymi polami. Brak cyfry nie musi oznaczać, że czarne pola są połączone; może być tylko brakiem informacji.
Poniższe zadanie jest dość trudne, więc dla zachęty jedna cyfra pojawiła się już na swoim miejscu. W rozwiązaniu wystarczy podać sumę cyfr i liczbę czarnych pól na przekątnych.


Komentarze
Po opisie zadania wnioskuję, że rząd oznacza kolumnę lub wiersz diagramu, tzn. rząd jest albo poziomy, albo pionowy.
Kluczem do rozwiązania jest wiersz z 14 oraz kolumny z 13. Wiemy bowiem, że w tych rzędach pomiędzy czarne kwadraty muszą trafić wszystkie liczby poza jedną (poza 1 w wierszu, poza 2 w kolumnach).
Zakładając dwa możliwe układy w wierszu z 14 możemy od razu uzupełnić kolumny z 13 i próbujemy rozwiązać oba warianty. Jeden z nich dość szybko prowadzi do jednoznacznego rozwiązania, drugi do sprzeczności.
Oto rozwiązanie:
2#345#1
#5124#3
532##14
41#532#
34##152
1#5324#
#241#35
Tym razem obyło się bez komputera 😀
Istnieją 2 rozwiązania, ale zawsze:
sumy na przekątnych = 6, 23
czarne na przekątnych = 5, 0
w lewym dolnym rogu jest czarny kwadrat
2x345x1
x5124x3
532xx14
41x532x
34xx152
1x5324x
x241x35
A drugie jakie?
mp
2x345x1
x5124x3
532xx14
41x532x
34xx152
1x5324x
x241x35
Suma cyfr na przekątnych: 24 + 6 (+5 czarnych) = 30 i 5 czarnych pól.
Machnąłem się w dodawaniu, prawdopodobnie pod koniec rozwiązywania zagadki, bo strukturę czarnych pól mam poprawną. Dwa rozwiązania byłyby wtedy, gdyby suma w dolnym rzędzie wynosiła 9.
Na przekątnych jest 5 czarnych pól i suma pól 25 lub 30 (5 na przecięciu przekątnych)
Na jednej przekatnej są same cyfry i ich suma wynosi 24, na drugiej jest 5 czarnych pól i dwie liczby o sumie 6.
Od razu widać, że z dwóch pierwszych kolumn jedna musi zaczynać się dwójką, a druga dwójką kończyć. Niestety trzeba wpisać przeszło połowę cyfr, aby doprowadzic do sprzeczności rozwiązanie z dwójką w lewym dolnym rogu.