Trasa
W kwietniowym Świecie Nauki, w dziale Umysł giętki, zamieściłem kilka zadań – jak zwykle, ale nieco trudniejszych niż zwykle. Prawie wszystkie miały charakter problemowy, w tym jedno było trochę podstępne. Nic więc dziwnego, że poprawnych rozwiązań przyszło niewiele. Ciekaw jestem, jak z jednym z tych zadań poradzą sobie Łamiblogowicze.
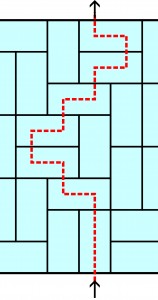
Na rysunku oznaczona jest trasa przejścia od jednego brzegu prostokąta z dominowym parkietażem do przeciwległego, poprowadzona zgodnie z następującą zasadą: po wejściu na domino należy przejść na jego drugą połowę, a następnie na sąsiednie domino, kierując się wprost ku docelowemu brzegowi.
Dla jakich prostokątów ułożonych z domina każda tak wytyczona trasa opuszcza parkietaż w tym samym rzędzie pionowym (jak na rysunku) lub poziomym, w którym się zaczęła? Albo inaczej: jaki warunek (konieczny i wystarczający) powinien być spełniony, aby wejście i wyjście było w tym samym rzędzie?

Komentarze
Chodzi o to, aby dla prostokąta o ustalonych wymiarach RxK (R rzędów, K kolumn) wyznaczyć jakie warunki musi spełniać parkietaż całego prostokąta, aby rozpoczynając wędrówkę z dowolnej kolumny zakończyć ją w tej samej kolumnie?
Proszę o potwierdzenie, czy poprawnie zrozumiałem postawione zadanie.
Tak, potwierdzam, ale… tak postawione pytanie jest trochę „podstępne” (nie całkiem ścisłe), dlatego w ostatnim zdaniu sformułowałem je nieco inaczej – „niepodstępnie” 🙂
mp
Postawię hipotezę:
Wejście i wyjście jest w tym samym rzędzie wtedy i tylko wtedy, gdy dla każdej pary sąsiadujących kolumn, liczba klepek ułożonych poziomo i znajdujących się w wybranych kolumnach jest parzysta.
Powyższe intuicyjnie wydaje się prawdziwe, ale jeszcze nie udało mi się tego udowodnić. Liczę, że jest ładny dowód potwierdzający prawdziwość tej hipotezy.
Strzelam:
Ilość domin prostopadłych do kierunku ruchu i przecinających go musi być parzysta.
Tak na szybkiego i na intuicję: suma odchyleń w lewo i w prawo powinna być równa ‚0’, a więc ustalając dla płytek poziomych ‚wysuniętych’ na lewo -1 a na prawo +1 i sumując je, jeśli wyjdzie zero to trasa zakończy sie w tym samym rzędzie….
Trochę to zawiłe, może da się wyartykułować prościej:
Warunkiem wystarczającym dla rozpatrywanej cechy jest to, aby każdy prostokąt był ułożony z klocków domina w taki sposób, aby każda kolumna zawierała parzystą ilość współśrodkowych klocków poziomych (niekoniecznie sąsiadujących ze sobą).
To może tak:
W każdym rzędzie (wierszu lub kolumnie) ilość klocków ułożonych prostopadle do kierunku poruszania się musi być parzysta.
Ten i niektóre z poprzednich propozycji warunków uwolniłem nie dlatego, że są błędne, ale dlatego, że są wtórne. Stanowią jakby wnioski z podstawowego warunku, który można sformułować w bardzo prosty sposób.
mp
Liczba kolumn i liczba wierszy musi być parzysta.
Prostokąt powinien mieć wymiary ‚parzyste’, tzn. boki musza mieć parzystą krotność krótszego boku domina.
Udało mi się udowodnić postawioną hipotezę uzyskując:
Twierdzenie:
Wejście i wyjście jest w tym samym rzędzie wtedy i tylko wtedy, gdy dla każdej pary sąsiadujących kolumn, liczba klepek ułożonych poziomo i znajdujących się w wybranych kolumnach jest parzysta.
Dowodu nie przedstawiam. Bazuje on na wyszukiwaniu prostokątów o szerokości 2 i wysokości n, w których górna i dolna klepka są poziome, pozostałe klepki są pionowe. W takim prostokącie można zmienić parkietaż tak, aby pozostały w nim same klepki pionowe. Po wykonaniu skończonej liczby modyfikacji parkietażu otrzymujemy prostokąt trywialny (tzn. wszystkie klepki są pionowe).
Każda taka zmiana parkietażu jest niezmiennikiem, zarówno układu wejścia/wyjścia do prostokąta każdej ścieżki, jak i parzystości klepek poziomych w każdej parze sąsiadujących kolumn.
Dowód z lewej strony do prawej poszukuje takich prostokątów bazując na ścieżce, w której następuje zmiana kolumny z x na x+1 lub x-1 a potem ponownie na x, przy czym poszukujemy takiej ścieżki i takiej zmiany, która jest najkrótsza w całym prostokącie.
Dowód z prawej strony do lewej rozpoczyna wyszukiwanie prostokątów od lewej strony dużego prostokąta, wybierając dwie pierwsze klepki poziome w skrajnej lewej kolumnie (która w ogóle zawiera jeszcze klepli poziome) i takie klepki wraz z klepkami pomiędzy nimi tworzą prostokąt 2xn którego szukamy, albo przesuwamy się o jedną kolumnę w prawo zastępując wybrane klepki poziome dwiema pierwszymi od góry klepkami znajdującymi się pomiędzy poprzenio wybranymi klepkami poziomymi. W razie potrzeby kontynuujemy przesuwanie się w prawo tak długo, aż nie natrafimy na szukany prostokąt.
Liczba pól (tj. długość prostokąta) w kierunku ruchu musi być parzysta.
Chyba wystarczy aby prostokąt miał parzystą ilość wierszy. Z pewnością jest to warunek konieczny. Ale zdaje się, że również wystarczający.
Mój 6-tygodniowy syn nie pozwolił mi dziś zmrużyc oka, dając jednocześnie trochę czasu do przemyśleń. I wymyśliłem!
Pokrętny warunek „każda para sąsiadujących kolumn zawiera parzystą liczbę klepek poziomych” jest równoważny nastepujacemu „wysokość prostokąta jest parzysta”. Dowód jest bardzo prosty…
Wszystkich programistów zachęcam do wzięcia udziału w Potyczkach Algorytmicznych:
http://potyczki.mimuw.edu.pl/
Konkurs startuje już jutro…
Wysokość prostokąta musi być wyrażona liczbą parzystą? No i oczywiście parkiet musi być skończony na bokach 😉
Miodziu, gratulacje (a propos 6 – tygodniowego syna)!
Moja dłuższa nieobecność na łamiblogu była spowodowana przez moją obecnie 6 – miesięczną córkę: zamiast mieć czas na nocne przemyślenia, po prostu nie miałem czasu na nic 😉 Po tym burzliwym okresie wszystko już wraca do ustalonego rytmu, więc nie przewiduję kolejnych przerw w łamiblogowaniu 🙂
@gpsE: dziękuję i również gratuluję córki. Ale nie wierz, że po pół roku córki będzie spokój… Wtedy dopiero zaczną się problemy, zęby, chodzenie, itp… Powodzenia 🙂